Torsion tensor
From Manifold Atlas
(Difference between revisions)
m |
|||
| Line 4: | Line 4: | ||
Let $M$ be a smooth manifold and $\nabla$ a [[Covariant derivative|covariant derivative]] on $TM$. | Let $M$ be a smooth manifold and $\nabla$ a [[Covariant derivative|covariant derivative]] on $TM$. | ||
Then the expression $T : \Gamma TM \times \Gamma TM \to \Gamma TM$, | Then the expression $T : \Gamma TM \times \Gamma TM \to \Gamma TM$, | ||
| − | + | \begin{equation} T(X,Y) = \nabla_XY -\nabla_YX - [X,Y] \end{equation} | |
for all vector fields $X,Y\in \Gamma TM$ is a [[Tensor|tensor]], called ''torsion tensor''. | for all vector fields $X,Y\in \Gamma TM$ is a [[Tensor|tensor]], called ''torsion tensor''. | ||
A covariant derivative $\nabla$ is called ''torsion free'' if $T = 0$. | A covariant derivative $\nabla$ is called ''torsion free'' if $T = 0$. | ||
In terms of coordinates, using a local parametrization $\phi : \R^n_o \to M$, the | In terms of coordinates, using a local parametrization $\phi : \R^n_o \to M$, the | ||
vanishing of the torsion means | vanishing of the torsion means | ||
| − | + | \begin{equation} \nabla_i\phi_j = \nabla_j\phi_i \end{equation} | |
for any $i,j = 1,\dots,n$ where $\nabla_i = \nabla_{\phi_i}$. | for any $i,j = 1,\dots,n$ where $\nabla_i = \nabla_{\phi_i}$. | ||
</wikitex> | </wikitex> | ||
| Line 16: | Line 16: | ||
[[Category:Definitions]] | [[Category:Definitions]] | ||
| + | [[Category:Connections and curvature]] | ||
Latest revision as of 10:52, 15 May 2013
|
The user responsible for this page is Jost Eschenburg. No other user may edit this page at present. |
|
This page has not been refereed. The information given here might be incomplete or provisional. |
1 Definition
Let  be a smooth manifold and
be a smooth manifold and  a covariant derivative on
a covariant derivative on  .
Then the expression
.
Then the expression 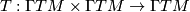 ,
,
(1)![T(X,Y) = \nabla_XY -\nabla_YX - [X,Y]](/images/math/5/3/c/53c5d2103998288c9253f916f737b7a7.png)
![T(X,Y) = \nabla_XY -\nabla_YX - [X,Y]](/images/math/5/3/c/53c5d2103998288c9253f916f737b7a7.png)
for all vector fields 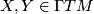 is a tensor, called torsion tensor.
A covariant derivative
is a tensor, called torsion tensor.
A covariant derivative  is called torsion free if
is called torsion free if 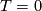 .
In terms of coordinates, using a local parametrization
.
In terms of coordinates, using a local parametrization 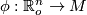 , the
vanishing of the torsion means
, the
vanishing of the torsion means
(2)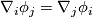
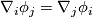
for any 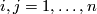 where
where 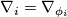 .
.