Thom spaces (Ex)
(Difference between revisions)
(Created page with "<wikitex>; {{beginthm|Exercise}} Let $X,X_1,X_2$ be $CW$-complexes and let $\xi,\xi_1,\xi_2$ be vector bundles over $X,X_1,X_2$ respectively. Denote by $\xi_1\times\xi_2$ th...") |
m |
||
| Line 12: | Line 12: | ||
{{beginthm|Exercise}} | {{beginthm|Exercise}} | ||
Let $\xi_k$ be the universal oriented vector bundle of rank $k$ | Let $\xi_k$ be the universal oriented vector bundle of rank $k$ | ||
| − | and let $(j_k,\overline{j_k})$: $\xi_k\oplus\mathbb{R}\to\xi_{k+1}$ be a bundle map. | + | and let $(j_k,\overline{j_k})$: $\xi_k\oplus\mathbb{R}\to\xi_{k+1}$ be a bundle map. Define |
| − | + | ||
| − | + | ||
| − | Define | + | |
$$ | $$ | ||
\gamma_k:=\mathrm{id}_X\times\xi_k,\quad | \gamma_k:=\mathrm{id}_X\times\xi_k,\quad | ||
(i_k,\overline{i_k}):=\mathrm{id}_X\times(j_k,\overline{j_k}). | (i_k,\overline{i_k}):=\mathrm{id}_X\times(j_k,\overline{j_k}). | ||
$$ | $$ | ||
| − | Show that for all $k\geq0$ we have $V_{k+1}\circ\Omega_n(\overline{i_k})=V_k$. Define | + | Show that for all $k\geq0$ we have $V_{k+1}\circ\Omega_n(\overline{i_k})=V_k$. |
| + | {{endthm}} | ||
| + | {{beginthm|Exercise}} | ||
| + | Define | ||
$$ | $$ | ||
\mathrm{Th}(\overline{i_k}):\quad \Sigma\mathrm{Th}(\gamma_k)\cong\mathrm{Th}(\gamma_k\oplus\mathbb{R})\to\mathrm{Th}(\gamma_{k+1}) | \mathrm{Th}(\overline{i_k}):\quad \Sigma\mathrm{Th}(\gamma_k)\cong\mathrm{Th}(\gamma_k\oplus\mathbb{R})\to\mathrm{Th}(\gamma_{k+1}) | ||
Revision as of 00:33, 27 March 2012
Exercise 0.1.
Let 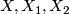 be
be 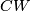 -complexes and let
-complexes and let 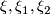 be vector bundles
over
be vector bundles
over 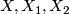 respectively.
Denote by
respectively.
Denote by 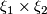 the product bundle over
the product bundle over 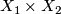 .
Find homeomorphisms
.
Find homeomorphisms
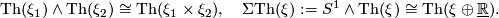
Exercise 0.2.
Let 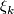 be the universal oriented vector bundle of rank
be the universal oriented vector bundle of rank 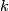 and let
and let 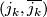 :
: 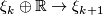 be a bundle map. Define
be a bundle map. Define
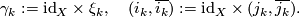
Show that for all 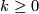 we have
we have 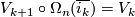 .
.
Exercise 0.3. Define
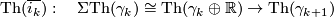
and
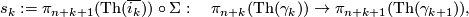
where 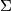 is the suspension homomorphism. Show that for all
is the suspension homomorphism. Show that for all 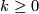 we have
we have 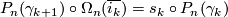 .
.
Question 0.4. Can we do similar things for unoriented manifolds, manifolds with spin structure,...?