Thickenings
m |
m |
||
| Line 1: | Line 1: | ||
{{Stub}}== Introduction == | {{Stub}}== Introduction == | ||
<wikitex>; | <wikitex>; | ||
| − | Let $K$ be a finite connected CW-complex of dimension $K$. For a given $n > k$ we would like to know if there is a compact manifold $M$ with boundary $\partial M$ such that: | + | Let $K$ be a finite connected CW-complex of dimension $K$. For a given $n = k + q > k$ we would like to know if there is a compact manifold $M$ with boundary $\partial M$ such that: |
# the map $\pi_1(\partial M) \to \pi_1(M)$ is an isomorphism, | # the map $\pi_1(\partial M) \to \pi_1(M)$ is an isomorphism, | ||
# $M$ is homotopy equivalent to $K$. | # $M$ is homotopy equivalent to $K$. | ||
| Line 21: | Line 21: | ||
& K} | & K} | ||
$$ | $$ | ||
| + | The set of isomorphism classes of $n$-dimensional $\Cat$-thickenings over $K$ is denoted | ||
| + | $$ \mathcal{T}^n(K) := \{ [\phi: K \simeq M ] \}. $$ | ||
{{endthm}} | {{endthm}} | ||
</wikitex> | </wikitex> | ||
| − | == | + | == Constructions and examples == |
| + | The simplest examples of thickenings come from $q$-disc bundles with sections over manifolds, $q > 2$. Let $X$ be a closed $\Cat$-manifold of dimension $k$, let $M \to W$ be a bundle with fibre $D^q$ and with section $s \colon M \to X$. | ||
| + | * the pair $(M, s)$ is an $n$-thickening of $X$. | ||
| + | ** the pair $(D^, pt)$ is an $n$-thickening of a point. | ||
| − | == Classification | + | == Invariants == |
| + | <wikitex>; | ||
| + | An important invariant of a thickening $(M, \phi)$ is the induced stable $\Cat$-bundle over $K$: | ||
| + | $$ T(M, \phi) = \phi^* TM $$ | ||
| + | where $TM \to M$ is the stable $\Cat$-tangent bundle of $M$. Given that stable bundles over the space $K$ are classified by maps to the classifying space $B\Cat$ one equivalently thinks of | ||
| + | $$ T(M, \phi) = [f_{TM} \circ \phi]$$ | ||
| + | where $f_{TM} : M \to B\Cat$ is the classifying map. | ||
| + | </wikitex> | ||
| + | == Classification == | ||
| + | <wikitex>; | ||
| + | An extremely useful classification theorem in manifold theory is the classification of ''stable thickenings'' where $n \geq 2k+1$ originally due to Wall in the smooth catagory. | ||
| + | {{beginthm|Theorem|\cite{} \cite{}}} | ||
| + | For all $n \geq k$, the stable classifying map gives rise to a set bijection | ||
| + | $$ \mathcal{T}^n(K) \equiv [K, B\Cat], \quad [M, \phi] \mapsto T(M, \phi) = [\phi \circ f_{TM}].$$ | ||
| + | {{endthm}} | ||
| + | </wikitex> | ||
== References == | == References == | ||
{{#RefList:}} | {{#RefList:}} | ||
| − | [[Category: | + | [[Category:Manifolds]] |
Revision as of 15:45, 27 November 2010
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
Let  be a finite connected CW-complex of dimension
be a finite connected CW-complex of dimension  . For a given
. For a given 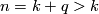 we would like to know if there is a compact manifold
we would like to know if there is a compact manifold  with boundary
with boundary 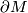 such that:
such that:
- the map
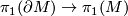 is an isomorphism,
is an isomorphism,
-
 is homotopy equivalent to
is homotopy equivalent to  .
.
In this case we say that  thickens
thickens  . If there is such a manifold
. If there is such a manifold  , we would like to know how many up to homeomorphism or diffeomorphism if
, we would like to know how many up to homeomorphism or diffeomorphism if  is smooth.
is smooth.
In [Wall1966a] Wall introduced the notion of a thickening, defined below, to investigate the questions raised above. This page summarizes the basis results concerning thickenings.
Recall that 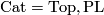 or
or 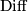 denotes respectively the topological, piecewise linear or smooth categories.
denotes respectively the topological, piecewise linear or smooth categories.
Definition 0.1 [Wall1966a, Section 1].
Let  be a finite connected CW complex. An
be a finite connected CW complex. An  -dimensional
-dimensional  -thickening of
-thickening of  consists of
consists of
- a compact
 -dimensional
-dimensional  -manifold
-manifold  with connected boundary such that
with connected boundary such that 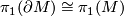
- a basepoint
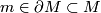 and an orientation of
and an orientation of 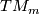 ,
,
- a simple homotopy equivalence
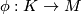 .
.
Two thickenings 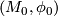 and
and 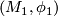 are isomorphic if there is a
are isomorphic if there is a  -isomorphism
-isomorphism 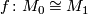 preserving
preserving  and the orientation of
and the orientation of 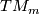 and such that
and such that  is simple homotopic to
is simple homotopic to 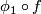 . In particular there is a simple homotopy commutative diagram:
. In particular there is a simple homotopy commutative diagram:
![\displaystyle \xymatrix{ M_0 \ar[dr]^{\phi_0} \ar[0,2]^{f} & & M_1 \ar[dl]_{\phi_1} \\ & K}](/images/math/e/7/b/e7b93f90388fbe391b8ba5e78d5a0abe.png)
The set of isomorphism classes of  -dimensional
-dimensional  -thickenings over
-thickenings over  is denoted
is denoted
![\displaystyle \mathcal{T}^n(K) := \{ [\phi: K \simeq M ] \}.](/images/math/6/f/2/6f2f2839b8992a717559a381a9424f72.png)
2 Constructions and examples
The simplest examples of thickenings come from $q$-disc bundles with sections over manifolds, $q > 2$. Let $X$ be a closed $\Cat$-manifold of dimension $k$, let $M \to W$ be a bundle with fibre $D^q$ and with section $s \colon M \to X$.
- the pair $(M, s)$ is an $n$-thickening of $X$.
- the pair $(D^, pt)$ is an $n$-thickening of a point.
3 Invariants
An important invariant of a thickening 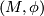 is the induced stable
is the induced stable  -bundle over
-bundle over  :
:
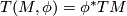
where 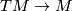 is the stable
is the stable  -tangent bundle of
-tangent bundle of  . Given that stable bundles over the space
. Given that stable bundles over the space  are classified by maps to the classifying space
are classified by maps to the classifying space 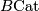 one equivalently thinks of
one equivalently thinks of
![\displaystyle T(M, \phi) = [f_{TM} \circ \phi]](/images/math/0/2/8/02809eaecaaddf353ed870a4aad4f046.png)
where 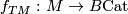 is the classifying map.
is the classifying map.
4 Classification
An extremely useful classification theorem in manifold theory is the classification of stable thickenings where 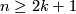 originally due to Wall in the smooth catagory.
originally due to Wall in the smooth catagory.
Theorem 3.1 \cite{} \cite{.}
For all 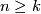 , the stable classifying map gives rise to a set bijection
, the stable classifying map gives rise to a set bijection
![\displaystyle \mathcal{T}^n(K) \equiv [K, B\Cat], \quad [M, \phi] \mapsto T(M, \phi) = [\phi \circ f_{TM}].](/images/math/e/0/3/e039e9b31f39a37e1a35602e33d50a7b.png)
5 References
- [Wall1966a] C. T. C. Wall, Classification problems in differential topology. IV. Thickenings, Topology 5 (1966), 73–94. MR0192509 (33 #734) Zbl 0149.20501