Tangent bundles of bundles (Ex)
(Difference between revisions)
m |
m |
||
| Line 6: | Line 6: | ||
where $T_{\pi}E$ consists of those tangent vectors tangent to the fibres of $\pi$. | where $T_{\pi}E$ consists of those tangent vectors tangent to the fibres of $\pi$. | ||
{{endthm}} | {{endthm}} | ||
| + | |||
| + | {{beginthem|Question}} | ||
| + | Is the bundle $T_{\pi}E$ the pullback of some bundle over $B$? | ||
| + | {{endthm}} | ||
| + | |||
{{beginthm|Exercise}} | {{beginthm|Exercise}} | ||
Suppose that $\pi \colon E \to B$ is itself a smooth vector bundle. Determine $TE$ in terms of $TB$ and $\pi$ regarded as a vector bundle. | Suppose that $\pi \colon E \to B$ is itself a smooth vector bundle. Determine $TE$ in terms of $TB$ and $\pi$ regarded as a vector bundle. | ||
{{endthm}} | {{endthm}} | ||
| + | |||
{{beginthm|Exercise}} | {{beginthm|Exercise}} | ||
Suppose that $\pi \colon E \to B$ is the sphere bundle of a vector bundle. Determine the stable tangent bundle of $E$ in terms of $\pi$ and $TB$. | Suppose that $\pi \colon E \to B$ is the sphere bundle of a vector bundle. Determine the stable tangent bundle of $E$ in terms of $\pi$ and $TB$. | ||
{{endthm}} | {{endthm}} | ||
| + | |||
{{beginthm|Exercise}} | {{beginthm|Exercise}} | ||
Compute the total Pontragin class of $\Hh P^n$, [[Wikipedia:Quaternionic_projective_space|quaternionicprojective space]]. (This was first achieved in {{citeD|Hirzebruch1953}}). | Compute the total Pontragin class of $\Hh P^n$, [[Wikipedia:Quaternionic_projective_space|quaternionicprojective space]]. (This was first achieved in {{citeD|Hirzebruch1953}}). | ||
Revision as of 18:03, 9 February 2012
Let 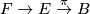 be a smooth fiber bundle so that all spaces
be a smooth fiber bundle so that all spaces 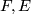 and
and  are manifolds.
are manifolds.
Exercise 0.1.
Show that 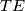 , the tangent bundle of
, the tangent bundle of  , splits as the sum of two bundles
, splits as the sum of two bundles
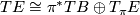
where 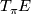 consists of those tangent vectors tangent to the fibres of
consists of those tangent vectors tangent to the fibres of  .
.
Template:Beginthem
Is the bundle 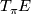 the pullback of some bundle over
the pullback of some bundle over  ?
</div>
?
</div>
Exercise 0.2.
Suppose that 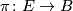 is itself a smooth vector bundle. Determine
is itself a smooth vector bundle. Determine 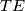 in terms of
in terms of 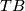 and
and  regarded as a vector bundle.
regarded as a vector bundle.
Exercise 0.3.
Suppose that 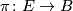 is the sphere bundle of a vector bundle. Determine the stable tangent bundle of
is the sphere bundle of a vector bundle. Determine the stable tangent bundle of  in terms of
in terms of  and
and 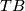 .
.
Exercise 0.4.
Compute the total Pontragin class of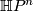 , quaternionicprojective space. (This was first achieved in [Hirzebruch1953]).
, quaternionicprojective space. (This was first achieved in [Hirzebruch1953]).