Talk:Whitehead torsion IV (Ex)
(Difference between revisions)
m |
|||
| Line 3: | Line 3: | ||
For the Whitehead torsion of $(i')^{-1}\circ i:M\rightarrow M'$ we have, using the quoted results of Milnor, | For the Whitehead torsion of $(i')^{-1}\circ i:M\rightarrow M'$ we have, using the quoted results of Milnor, | ||
$$\tau\left((i')^{-1}\circ i\right)=-\tau(W,M')+\tau(W,M)=(-1)^{2k+1}\hat\tau(W,M)+\tau(W,M)=-\tau(W,M)+\tau(W,M)=0$$ | $$\tau\left((i')^{-1}\circ i\right)=-\tau(W,M')+\tau(W,M)=(-1)^{2k+1}\hat\tau(W,M)+\tau(W,M)=-\tau(W,M)+\tau(W,M)=0$$ | ||
| − | So on the boundary $M$ of $W$ we have for $f|_M=(i')^{-1}\circ i: | + | So on the boundary $M$ of $W$ we have for $f|_M=(i')^{-1}\circ i:M\rightarrow M'$ that $\tau(f|_{M})=0$. |
Since the odd-dimensional L-groups $L_{2k+1}^s(\Zz\pi)$ vanish for finite groups $\pi$ of odd order there is no obstruction to do surgeries in the interior of $W$ to turn it into an s-cobordism without changing the boundary. Thus $M$ and $M'$ are s-cobordant. | Since the odd-dimensional L-groups $L_{2k+1}^s(\Zz\pi)$ vanish for finite groups $\pi$ of odd order there is no obstruction to do surgeries in the interior of $W$ to turn it into an s-cobordism without changing the boundary. Thus $M$ and $M'$ are s-cobordant. | ||
</wikitex> | </wikitex> | ||
Revision as of 13:36, 29 March 2012
Let ![\varphi:W\rightarrow [0,1]](/images/math/8/e/2/8e2966ae1b64525ae0388f180897f3e9.png) a Morse function with
a Morse function with 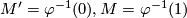 . We define
. We define 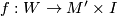 by
by 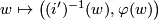 .
For the Whitehead torsion of
.
For the Whitehead torsion of 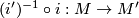 we have, using the quoted results of Milnor,
we have, using the quoted results of Milnor,
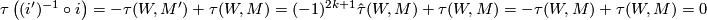
So on the boundary  of
of  we have for
we have for 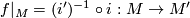 that
that 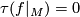 .
Since the odd-dimensional L-groups
.
Since the odd-dimensional L-groups 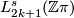 vanish for finite groups
vanish for finite groups  of odd order there is no obstruction to do surgeries in the interior of
of odd order there is no obstruction to do surgeries in the interior of  to turn it into an s-cobordism without changing the boundary. Thus
to turn it into an s-cobordism without changing the boundary. Thus  and
and 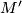 are s-cobordant.
are s-cobordant.