Whitehead torsion IV (Ex)
The aim of this exercise is to prove the following:
Proposition 0.1.
Let 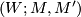 be an h-coborism between closed, connected
be an h-coborism between closed, connected 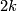 -manifolds with with finite abelian fundamental groups of odd order. If
-manifolds with with finite abelian fundamental groups of odd order. If 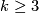 then
then  and
and 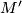 are s-cobordant.
are s-cobordant.
You may also wish to investigate possible extensions of this proposition.
[edit] Comments
The following results from [Milnor1966] will be helpful. Recall that the canonical involution on the group ring ![\Zz[\pi]](/images/math/5/9/a/59abcee2c0404c04e89fb508a53c9890.png) of a finitely generated group
of a finitely generated group  induces a conjuation on the Whitehead group.
induces a conjuation on the Whitehead group.
Lemma 2.1 [Milnor1966, Lemma 6.7] .
If  is finite abelian, then every element of
is finite abelian, then every element of 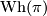 is self-conjugate.
is self-conjugate.
Theorem 2.2 [Milnor1966, Duality Theorem] .
For any orientable h-cobordism 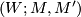 of dimension
of dimension  we have
we have
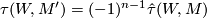
where 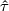 denotes the conjugate of
denotes the conjugate of  .
.
Now if 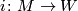 and
and 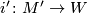 denote the inclusions, compute the Whitehead torsion of the homotopy equivalence
denote the inclusions, compute the Whitehead torsion of the homotopy equivalence 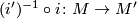 .
.
Finally, you may use the following theorem of Bak.
Theorem 2.3 c.f.[Bak1975, Theorem 1].
Let  be a finite group of odd order, then
be a finite group of odd order, then ![L_{1}^s(\Zz[\pi]) = L_3^s(\Zz[\pi]) = 0](/images/math/9/9/6/996aea5da261296d1eada1fa6a0d2aee.png) .
.
[edit] References
- [Bak1975] A. Bak, Odd dimension surgery groups of odd torsion groups vanish, Topology 14 (1975), no.4, 367–374. MR0400263 (53 #4098) Zbl 0322.57021
- [Milnor1966] J. Milnor, Whitehead torsion, Bull. Amer. Math. Soc. 72 (1966), 358–426. MR0196736 (33 #4922) Zbl 0147.23104