Talk:Tangent bundles of bundles (Ex)
Solution 0.1.
There is a short exact sequence of vector bundles over 
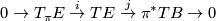
where  is the inclusion and
is the inclusion and  is defined by
is defined by 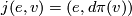 . We choose a Riemannian metric on
. We choose a Riemannian metric on 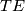 , then the orthogonal projection to
, then the orthogonal projection to 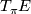 gives a splitting of the exact sequence. Which implies that
gives a splitting of the exact sequence. Which implies that
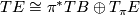
Solution 0.2.
A necessary condition for 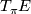 being the pullback of some bundle over
being the pullback of some bundle over  is that
is that 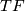 is trivial. This is seen by restricting the bundle to a point in
is trivial. This is seen by restricting the bundle to a point in  . On the other hand, obviously when
. On the other hand, obviously when  is a vector bundle or the bundle
is a vector bundle or the bundle 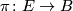 is trivial then
is trivial then 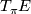 is the pullback of a vector bundle over
is the pullback of a vector bundle over  . We don't know if this is true in general.
. We don't know if this is true in general.
Solution 0.3.
If 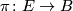 is itself a smooth vector bundle, then
is itself a smooth vector bundle, then 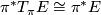 , therefore
, therefore 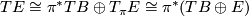 .
.
Solution 0.4.
Denote the associated vector bundle by  with projection
with projection 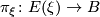 , then
, then 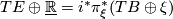 , where
, where 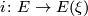 is the inclusion of the sphere bundle into the vector bundle.
is the inclusion of the sphere bundle into the vector bundle.
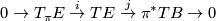
where  is the inclusion and
is the inclusion and  is defined by
is defined by 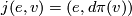 . We choose a Riemannian metric on
. We choose a Riemannian metric on 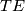 , then the orthogonal projection to
, then the orthogonal projection to 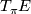 gives a splitting of the exact sequence. Which implies that
gives a splitting of the exact sequence. Which implies that
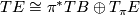
Solution 0.2.
A necessary condition for 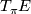 being the pullback of some bundle over
being the pullback of some bundle over  is that
is that 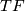 is trivial. This is seen by restricting the bundle to a point in
is trivial. This is seen by restricting the bundle to a point in  . On the other hand, obviously when
. On the other hand, obviously when  is a vector bundle or the bundle
is a vector bundle or the bundle 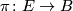 is trivial then
is trivial then 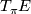 is the pullback of a vector bundle over
is the pullback of a vector bundle over  . We don't know if this is true in general.
. We don't know if this is true in general.
Solution 0.3.
If 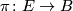 is itself a smooth vector bundle, then
is itself a smooth vector bundle, then 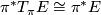 , therefore
, therefore 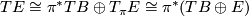 .
.
Solution 0.4.
Denote the associated vector bundle by  with projection
with projection 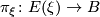 , then
, then 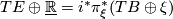 , where
, where 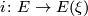 is the inclusion of the sphere bundle into the vector bundle.
is the inclusion of the sphere bundle into the vector bundle.