Talk:Surgery obstruction map I (Ex)
(Created page with "<wikitex>; We take $X=\mathbb H P^2$ and consider various bundle reductions of the normal bundle: The normal map $id_X$ gives the base point of $\mathcal N (X)$. The surgery o...") |
|||
| Line 1: | Line 1: | ||
<wikitex>; | <wikitex>; | ||
We take $X=\mathbb H P^2$ and consider various bundle reductions of the normal bundle: | We take $X=\mathbb H P^2$ and consider various bundle reductions of the normal bundle: | ||
| − | The normal map $id_X$ gives the base point of $\mathcal N (X)$. | + | The normal map $id_X$ gives the base point of $\mathcal N (X)\cong [X,G/TOP]$. |
| − | The surgery obstruction of a normal map $M\to X$ covered by $\nu_M\to \ | + | An element of $[X,G/TOP]$ is given by a bundle $\xi$ together with a fiber homotopy trivialization $\phi$. |
| − | $$ sign(M)-sign(X)=\langle L(-\ | + | Under the isomorphism $\mathcal N (X) \cong [X,G/O]$, the pair $(\xi,\phi)$ corresponds to a normal map $M\to X$ covered by $\nu_M\to \nu_X\oplus \xi$. |
| + | The surgery obstruction of a normal map $M\to X$ covered by $\nu_M\to \eta$ equals | ||
| + | $$ sign(M)-sign(X)=\langle L(-\eta),[X]\rangle -1,$$ | ||
so it depends only on the bundle over $X$. | so it depends only on the bundle over $X$. | ||
There are fiber homotopically trivial bundles on $X$ corresponding to classes in $[X,G/TOP]$ | There are fiber homotopically trivial bundles on $X$ corresponding to classes in $[X,G/TOP]$ | ||
| Line 9: | Line 11: | ||
collapses. | collapses. | ||
From [[Fibre_homotopy_trivial_bundles_(Ex)|another exercise]] we know that on $S^4$ we have such vector bundles with first Pontryagin class $48k$ times the generator of $H^4(S^4)$. | From [[Fibre_homotopy_trivial_bundles_(Ex)|another exercise]] we know that on $S^4$ we have such vector bundles with first Pontryagin class $48k$ times the generator of $H^4(S^4)$. | ||
| − | This means that on $X$ we have vector | + | This means that on $X$ we have a vector bundle $\xi$ with $p_1(\xi)=48$ whose sphere bundle is fiber homotopically trivial, by a fiber homotopy equivalence $\phi$. |
| − | $\mathcal N (X)=[X,G/O]$ with respect to the Whitney sum. | + | Now $(\xi\oplus\xi,\phi * \phi)$ is the sum of $(\xi,\phi)$ and $(\xi,\phi)$ in $\mathcal N (X)=[X,G/O]$ with respect to the Whitney sum. |
| − | + | We compute | |
| − | $$\sigma(\ | + | $$\sigma(-(\xi,-\phi))+\sigma(-(\xi,\phi)) - \sigma(-(\xi\oplus\xi,\phi * \phi)) |
| − | = \langle L(TX\oplus\ | + | = 2 \langle L(TX\oplus\xi), [X] \rangle - \langle L(TX\oplus\xi\oplus\xi), [X] \rangle -1 |
| − | + | = c \langle p_1(\xi)^2 ,[X] \rangle \ne 0$, $$ | |
| + | and so the surgery obstruction is not a group homomorphism with respect to the Whitney sum. | ||
</wikitex> | </wikitex> | ||
Revision as of 22:44, 29 May 2012
We take 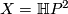 and consider various bundle reductions of the normal bundle:
The normal map
and consider various bundle reductions of the normal bundle:
The normal map 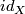 gives the base point of
gives the base point of ![\mathcal N (X)\cong [X,G/TOP]](/images/math/3/c/b/3cb550e2803532379ac40fb661b9a037.png) .
An element of
.
An element of ![[X,G/TOP]](/images/math/a/5/9/a59043680a03e05a031ee66e532a733d.png) is given by a bundle
is given by a bundle  together with a fiber homotopy trivialization
together with a fiber homotopy trivialization  .
Under the isomorphism
.
Under the isomorphism ![\mathcal N (X) \cong [X,G/O]](/images/math/a/0/4/a04f358c13c1b5bf493e750af395b740.png) , the pair
, the pair 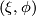 corresponds to a normal map
corresponds to a normal map 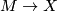 covered by
covered by 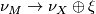 .
The surgery obstruction of a normal map
.
The surgery obstruction of a normal map 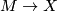 covered by
covered by 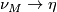 equals
equals
![\displaystyle sign(M)-sign(X)=\langle L(-\eta),[X]\rangle -1,](/images/math/b/f/5/bf5f39283eca20374368fe2303a87be4.png)
so it depends only on the bundle over  .
There are fiber homotopically trivial bundles on
.
There are fiber homotopically trivial bundles on  corresponding to classes in
corresponding to classes in ![[X,G/TOP]](/images/math/a/5/9/a59043680a03e05a031ee66e532a733d.png) which restrict to any given class in
which restrict to any given class in ![[S^4,G/Top]](/images/math/8/1/e/81e2e43bc8b0a3653245d764a879b54a.png) , since the corresponding Atiyah-Hirzebruch spectral sequence
collapses.
From another exercise we know that on
, since the corresponding Atiyah-Hirzebruch spectral sequence
collapses.
From another exercise we know that on  we have such vector bundles with first Pontryagin class
we have such vector bundles with first Pontryagin class 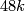 times the generator of
times the generator of 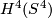 .
This means that on
.
This means that on  we have a vector bundle
we have a vector bundle  with
with 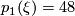 whose sphere bundle is fiber homotopically trivial, by a fiber homotopy equivalence
whose sphere bundle is fiber homotopically trivial, by a fiber homotopy equivalence  .
Now
.
Now 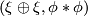 is the sum of
is the sum of 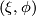 and
and 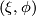 in
in ![\mathcal N (X)=[X,G/O]](/images/math/0/2/d/02dc86908e2973444cf8bd7d9a81f3c5.png) with respect to the Whitney sum.
We compute
with respect to the Whitney sum.
We compute
Tex syntax error
and so the surgery obstruction is not a group homomorphism with respect to the Whitney sum.