Talk:Obstruction classes and Pontrjagin classes (Ex)
(Created page with '== Desdirata for this page == Ideally this page will also include at least the following information: # A reference, probably to Baues' book, for obstructions to null-homotopy. #…') |
m |
||
| (4 intermediate revisions by one user not shown) | |||
| Line 1: | Line 1: | ||
| − | == | + | == Answer == |
| + | <wikitex>; | ||
| + | Let $a_j = (3 - (-1)^j)/2$, let $k!$ be the integer k-factorial and recall that $x \in H^{4i}(S^{4i})$ is a generator. | ||
| + | {{beginthm|Theorem|{{cite|Kervaire1959}}}} \label{thm:1} | ||
| + | There is an identity | ||
| + | $$ p_i(\xi^{4i}) = \pm a_i \cdot (2i-1)! \cdot x \in H^{4i}(S^{4i}).$$ | ||
| + | |||
| + | Similarly, if $\eta$ denotes the complex vector bundle over $S^{2i}$ corresponding to a generator of $\pi_{2i}(BU)\cong \mathbb{Z}$, then its Chern class is given by | ||
| + | $$ c_i(\eta) = \pm (i-1)! \cdot y\in H^{2i}(S^{2i}),$$ | ||
| + | where $y\in H^{2i}(S^{2i})\cong \mathbb{Z}$ is a generator. | ||
| + | {{endthm|Theorem}} | ||
| + | === Justification === | ||
| + | A way to prove the Theorem \ref{thm:1} is to use the Chern character | ||
| + | $$\tilde K_0(X)\to \tilde H^{ev}(X;\mathbb{Q})$$ | ||
| + | from complex topological $K$-theory. It can be defined using the explicit formula | ||
| + | $$ ch(\xi)= \sum_{k>0} s_k(c_1(\xi),\dots,c_k(\xi))/k! $$ | ||
| + | for a virtual complex vector bundle $\xi$, where $s_k$ are the [[Newton polynomials]]. In the case $X=S^{2n}$ two special things occur: | ||
| + | |||
| + | #The Chern character is injective with image $H^{2n}(S^{2n};\mathbb{Q})$. This follows from the case $n=1$ using Bott periodicity and multiplicativity: $$ \tilde K_0(S^{2n}) \cong\tilde K_0(S^2)\otimes \dots \otimes\tilde K_0(S^2) \to \tilde H^{ev}(S^{2};\mathbb{Q})\otimes \dots \otimes \tilde H^{ev}(S^{2};\mathbb{Q})\cong \tilde H^{ev}(S^{2n};\mathbb{Q}) $$ | ||
| + | #A calculation shows that the image of a (virtual) complex vector bundle $\xi$ over $S^{2n}$ is given by: | ||
| + | $$ch(\xi)= s_n(0,\dots, 0, c_n(\xi))/n! = \pm c_n(\xi)/(n-1)!$$ | ||
| + | |||
| + | Hence, $c_i(\eta)$ is given by $\pm (n-1)!$ times a generator. This establishes the second part of the Theorem. | ||
| + | |||
| + | The first part follows using the definition $p_i(\xi)= (-1)^ic_{2i}(\xi\otimes_\mathbb{R} \mathbb{C})$ together with the fact that complexification induces a map | ||
| + | $$ - \otimes_\mathbb{R} \mathbb{C}\colon \widetilde{KO}^0(S^{4i})\to \tilde K^0(S^{4i}) $$ | ||
| + | which is given by multiplication by $a_i$, i.e. is a isomorphism in degrees $8i$ and multiplication by 2 in degrees $8i+4$. | ||
| + | </wikitex> | ||
| + | |||
| + | == Further discussion == | ||
| + | <wikitex>; | ||
| + | The integrality condition for the Chern character (and the additional factor of 2 for complexifications of real vector bundles in dimensions $8i+4$) also follows from the Atiyah-Singer Index Theorem. | ||
| + | </wikitex> | ||
| + | |||
| + | == Desiderata for this page == | ||
Ideally this page will also include at least the following information: | Ideally this page will also include at least the following information: | ||
# A reference, probably to Baues' book, for obstructions to null-homotopy. | # A reference, probably to Baues' book, for obstructions to null-homotopy. | ||
# A precise reference to {{cite|Kervaire1959}}. | # A precise reference to {{cite|Kervaire1959}}. | ||
# A precise reference to Bott who also proved Theorem 2.1 (perhaps even before Kervaire?) | # A precise reference to Bott who also proved Theorem 2.1 (perhaps even before Kervaire?) | ||
| + | # Conventions/constructions for settling the sign in Theorem 2.1. | ||
# A reference to Husemoller's Fibre Bundles for a similar result for Chern classes. This also gives an explanation of the result via the Chern character which should be included in the page. | # A reference to Husemoller's Fibre Bundles for a similar result for Chern classes. This also gives an explanation of the result via the Chern character which should be included in the page. | ||
# Further discussion about the same problem for other characteristic classes and other bases spaces. | # Further discussion about the same problem for other characteristic classes and other bases spaces. | ||
[[User:Diarmuid Crowley|Diarmuid Crowley]] 16:21, 17 March 2010 (UTC) | [[User:Diarmuid Crowley|Diarmuid Crowley]] 16:21, 17 March 2010 (UTC) | ||
| + | |||
| + | == References == | ||
| + | {{#RefList:}} | ||
Latest revision as of 13:08, 9 February 2012
Contents |
[edit] 1 Answer
Let 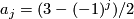 , let
, let 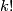 be the integer k-factorial and recall that
be the integer k-factorial and recall that 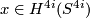 is a generator.
is a generator.
Theorem 1.1 [Kervaire1959]. There is an identity
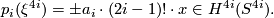
Similarly, if 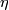 denotes the complex vector bundle over
denotes the complex vector bundle over 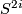 corresponding to a generator of
corresponding to a generator of 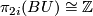 , then its Chern class is given by
, then its Chern class is given by
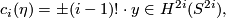
where 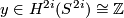 is a generator.
is a generator.
[edit] Justification
A way to prove the Theorem 1.1 is to use the Chern character
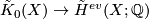
from complex topological  -theory. It can be defined using the explicit formula
-theory. It can be defined using the explicit formula
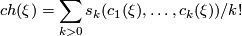
for a virtual complex vector bundle  , where
, where 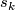 are the Newton polynomials. In the case
are the Newton polynomials. In the case 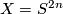 two special things occur:
two special things occur:
- The Chern character is injective with image
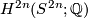 . This follows from the case
. This follows from the case  using Bott periodicity and multiplicativity:
using Bott periodicity and multiplicativity: 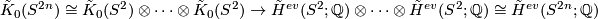
- A calculation shows that the image of a (virtual) complex vector bundle
 over
over 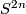 is given by:
is given by:
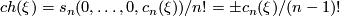
Hence, 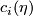 is given by
is given by 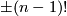 times a generator. This establishes the second part of the Theorem.
times a generator. This establishes the second part of the Theorem.
The first part follows using the definition 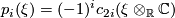 together with the fact that complexification induces a map
together with the fact that complexification induces a map
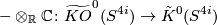
which is given by multiplication by 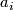 , i.e. is a isomorphism in degrees
, i.e. is a isomorphism in degrees 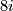 and multiplication by 2 in degrees
and multiplication by 2 in degrees 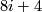 .
.
[edit] 2 Further discussion
The integrality condition for the Chern character (and the additional factor of 2 for complexifications of real vector bundles in dimensions 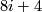 ) also follows from the Atiyah-Singer Index Theorem.
) also follows from the Atiyah-Singer Index Theorem.
[edit] 3 Desiderata for this page
Ideally this page will also include at least the following information:
- A reference, probably to Baues' book, for obstructions to null-homotopy.
- A precise reference to [Kervaire1959].
- A precise reference to Bott who also proved Theorem 2.1 (perhaps even before Kervaire?)
- Conventions/constructions for settling the sign in Theorem 2.1.
- A reference to Husemoller's Fibre Bundles for a similar result for Chern classes. This also gives an explanation of the result via the Chern character which should be included in the page.
- Further discussion about the same problem for other characteristic classes and other bases spaces.
Diarmuid Crowley 16:21, 17 March 2010 (UTC)
[edit] 4 References
- [Kervaire1959] M. A. Kervaire, A note on obstructions and characteristic classes, Amer. J. Math. 81 (1959), 773–784. MR0107863 (21 #6585) Zbl 0124.16302