Talk:Obstruction classes and Pontrjagin classes (Ex)
Contents |
[edit] 1 Answer
Let 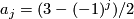 , let
, let 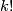 be the integer k-factorial and recall that
be the integer k-factorial and recall that 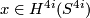 is a generator.
is a generator.
Theorem 1.1 [Kervaire1959]. There is an identity
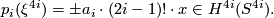
Similarly, if 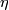 denotes the complex vector bundle over
denotes the complex vector bundle over 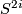 corresponding to a generator of
corresponding to a generator of 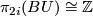 , then its Chern class is given by
, then its Chern class is given by
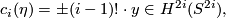
where 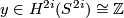 is a generator.
is a generator.
[edit] Justification
A way to prove the Theorem 1.1 is to use the Chern character
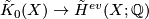
from complex topological  -theory. It can be defined using the explicit formula
-theory. It can be defined using the explicit formula
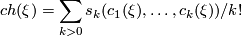
for a virtual complex vector bundle  , where
, where 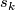 are the Newton polynomials. In the case
are the Newton polynomials. In the case 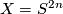 two special things occur:
two special things occur:
- The Chern character is injective with image
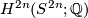 . This follows from the case
. This follows from the case  using Bott periodicity and multiplicativity:
using Bott periodicity and multiplicativity: 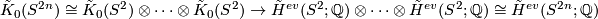
- A calculation shows that the image of a (virtual) complex vector bundle
 over
over 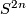 is given by:
is given by:
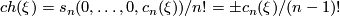
Hence, 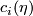 is given by
is given by 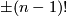 times a generator. This establishes the second part of the Theorem.
times a generator. This establishes the second part of the Theorem.
The first part follows using the definition 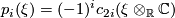 together with the fact that complexification induces a map
together with the fact that complexification induces a map
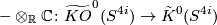
which is given by multiplication by 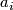 , i.e. is a isomorphism in degrees
, i.e. is a isomorphism in degrees 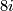 and multiplication by 2 in degrees
and multiplication by 2 in degrees 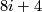 .
.
[edit] 2 Further discussion
The integrality condition for the Chern character (and the additional factor of 2 for complexifications of real vector bundles in dimensions 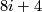 ) also follows from the Atiyah-Singer Index Theorem.
) also follows from the Atiyah-Singer Index Theorem.
[edit] 3 Desiderata for this page
Ideally this page will also include at least the following information:
- A reference, probably to Baues' book, for obstructions to null-homotopy.
- A precise reference to [Kervaire1959].
- A precise reference to Bott who also proved Theorem 2.1 (perhaps even before Kervaire?)
- Conventions/constructions for settling the sign in Theorem 2.1.
- A reference to Husemoller's Fibre Bundles for a similar result for Chern classes. This also gives an explanation of the result via the Chern character which should be included in the page.
- Further discussion about the same problem for other characteristic classes and other bases spaces.
Diarmuid Crowley 16:21, 17 March 2010 (UTC)
[edit] 4 References
- [Kervaire1959] M. A. Kervaire, A note on obstructions and characteristic classes, Amer. J. Math. 81 (1959), 773–784. MR0107863 (21 #6585) Zbl 0124.16302