Talk:Normal maps - (non)-examples (Ex)
1) First note that, for any closed manifold  , there is a map
, there is a map 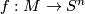 giving by contracting the complement of an embedded disc
giving by contracting the complement of an embedded disc 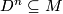 . At a point
. At a point 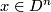 , this map is bijective and has local degree
, this map is bijective and has local degree 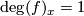 and so
and so 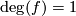 by the fact that the degree is the sum of local degrees, i.e.
by the fact that the degree is the sum of local degrees, i.e. 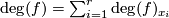 where
where 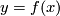 and
and 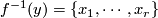 which in this case is just
which in this case is just 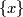 .
.
Now specialise to the case 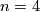 and
and 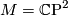 ,
, 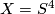 and consider
and consider 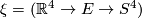 , an arbitrary 4-dimensional real vector bundle over
, an arbitrary 4-dimensional real vector bundle over 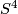 . If there is a normal map
. If there is a normal map 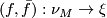 then, since this is a fibrewise isomorphism we must have that
then, since this is a fibrewise isomorphism we must have that 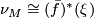 . Consider the first Pontryagin classes
. Consider the first Pontryagin classes 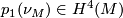 and
and 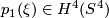 . With respect to some identifications
. With respect to some identifications 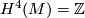 and
and 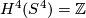 , we will show that
, we will show that 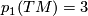 and
and 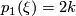 for some
for some 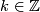 which will depend on the choice of bundle
which will depend on the choice of bundle  .
.
This would complete the proof since this would imply that 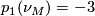 but also that
but also that 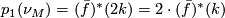 which is divisible by two. Note that that fact that
which is divisible by two. Note that that fact that 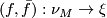 is only a stable bundle map is dealt with here by the fact that
is only a stable bundle map is dealt with here by the fact that 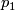 is a stable bundle invariant and so gives that same construction for any two stably isomorphic bundles of the same dimension.
is a stable bundle invariant and so gives that same construction for any two stably isomorphic bundles of the same dimension.
To show that 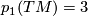 for
for 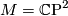 and some choice of identification
and some choice of identification 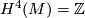 , we can use a number of techniques. One quick trick is to note that the Hirzebruch Signature Theorem applies to
, we can use a number of techniques. One quick trick is to note that the Hirzebruch Signature Theorem applies to  and gives that
and gives that ![\sigma(M) =\frac{1}{3} p_1(TM)[M]](/images/math/4/d/a/4da72ae5bd441a85e40dff8d6245227d.png) by the fact that the first polynomial is the multiplicative sequence corresponding to the
by the fact that the first polynomial is the multiplicative sequence corresponding to the  -genus is
-genus is 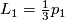 . Now
. Now 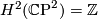 and the intersection form is
and the intersection form is 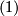 gives that
gives that 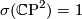 and so
and so ![p_1(TM)[M] =3](/images/math/4/9/7/497b22c8074202e4510529b77c6281f0.png) . Hence
. Hence 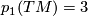 with appropriate identifications. Another, more elementary, method is to show that
with appropriate identifications. Another, more elementary, method is to show that 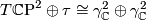 where
where 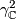 is the tautological complex line bundle over
is the tautological complex line bundle over 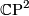 . This allows us to compute the total Chern class immediately which can then be used to recover the Pontryagin classes using the the highly useful formula
. This allows us to compute the total Chern class immediately which can then be used to recover the Pontryagin classes using the the highly useful formula 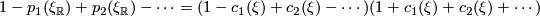 where
where 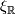 denotes that fibrewise replacement of
denotes that fibrewise replacement of 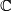 with
with 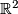 .
.
To show that 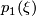 is always even is more tricky, and is asserted (but not proven) in Milnor's paper which proves the existence of exotic
is always even is more tricky, and is asserted (but not proven) in Milnor's paper which proves the existence of exotic  -spheres. Firstly let
-spheres. Firstly let 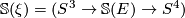 be the sphere bundle corresponding to
be the sphere bundle corresponding to  . Recall that, by clutching construction for bundles over spheres, there is a 1-1 correspondence between fibre bundles over
. Recall that, by clutching construction for bundles over spheres, there is a 1-1 correspondence between fibre bundles over  with fixed fibre
with fixed fibre  and structure group
and structure group  and
and 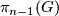 . Hence oriented
. Hence oriented  -bundles over
-bundles over 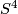 are classified by
are classified by 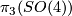 . One can show explicitly that
. One can show explicitly that 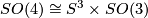 and so has universal cover
and so has universal cover 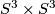 and therefore
and therefore 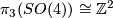 since covering maps induce isomorphisms on higher homotopy groups. Fix an explicit identification of
since covering maps induce isomorphisms on higher homotopy groups. Fix an explicit identification of 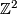 with
with 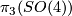 . Therefore
. Therefore 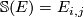 where
where 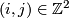 labels the element of
labels the element of 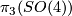 corresponding to the sphere bundle.
corresponding to the sphere bundle.
There is a map 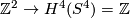 given by mapping
given by mapping 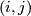 to
to 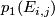 . By considering the inclusion of the fibre of the corresponding real vector bundle into the total space, one can show that this map factors as group homomorphisms
. By considering the inclusion of the fibre of the corresponding real vector bundle into the total space, one can show that this map factors as group homomorphisms 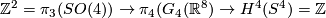 where
where 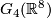 is the Grassmannian , i.e. the
is the Grassmannian , i.e. the  -dimensional linear subspaces of
-dimensional linear subspaces of 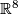 . Hence
. Hence 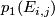 is linear in
is linear in  and
and  and so of the form
and so of the form 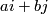 . By considering the quaternionic conjugate on the fibre, we can also show that
. By considering the quaternionic conjugate on the fibre, we can also show that 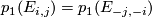 which guarantees that
which guarantees that 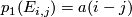 for some
for some 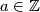 and some identification
and some identification 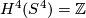 . To finish, we can check that
. To finish, we can check that 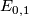 is the tautological bundle over
is the tautological bundle over 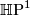 by using an explicit identification of
by using an explicit identification of 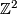 with
with 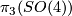 . This shows that
. This shows that 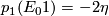 where
where 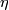 is the pullback of the chosen generator of
is the pullback of the chosen generator of 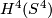 along an identification
along an identification 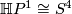 . This shows that
. This shows that 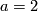 and hence
and hence 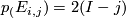 which completes the proof.
which completes the proof.
See also Obstruction classes and Pontrjagin classes (Ex).
2) For any  , let
, let 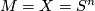 . Note that the stable normal bundle
. Note that the stable normal bundle 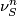 is trivial since the normal bundle of the codimension one embedding
is trivial since the normal bundle of the codimension one embedding 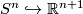 is trivial. Hence any map
is trivial. Hence any map 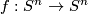 extends to a bundle map
extends to a bundle map 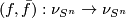 and so it suffices to find degree
and so it suffices to find degree  maps
maps 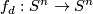 for any
for any  .
.
For  , a degree
, a degree  map
map 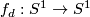 is given by wrapping the circle
is given by wrapping the circle  times around itself. By suspending
times around itself. By suspending  times we get a map
times we get a map 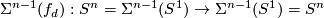 which we can show still has degree
which we can show still has degree  by using local degrees as in the previous exercise.
by using local degrees as in the previous exercise.
3) We will show that there is a degree one normal map 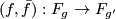 if and only if
if and only if 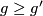 . Firstly note that, as above, the codimension one embedding
. Firstly note that, as above, the codimension one embedding 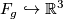 is trivial and so
is trivial and so 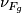 is trivial for all
is trivial for all  . Hence any map extends to a normal map and it remains to show that there is a degree one map
. Hence any map extends to a normal map and it remains to show that there is a degree one map 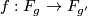 if and only if
if and only if 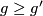 .
.
If 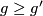 , then we can get a map
, then we can get a map 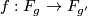 by contracting the complement of the standard
by contracting the complement of the standard 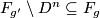 . This is degree one using local degree as in the first exercise.
. This is degree one using local degree as in the first exercise.
Let 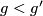 and suppose there is a map
and suppose there is a map 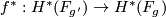 of cohomology rings sending the generator of
of cohomology rings sending the generator of 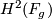 to the generator of
to the generator of 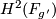 . Note that
. Note that 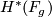 is generated by
is generated by 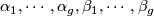 in degree one and
in degree one and 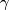 is degree two such that
is degree two such that 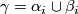 for
for 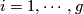 and all other products of the degree one generators zero. This can be lifted from the quotient map
and all other products of the degree one generators zero. This can be lifted from the quotient map 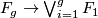 and the structure of the cohomology ring of
and the structure of the cohomology ring of 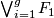 coming from that of
coming from that of 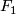 . Since
. Since 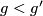 , the map
, the map 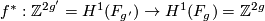 has a non-zero element
has a non-zero element 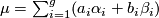 in its kernel. Suppose, without loss of generality, that
in its kernel. Suppose, without loss of generality, that 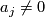 . Then
. Then 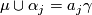 and so
and so 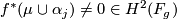 . However
. However 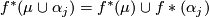 and
and 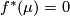 by hypothesis. This is a contradiction.
by hypothesis. This is a contradiction.
This can also be proven by using that a degree one map 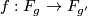 induces a surjection
induces a surjection 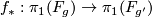 and so a surjection
and so a surjection 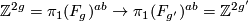 which gives a contradiction as before.
which gives a contradiction as before.
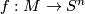 giving by contracting the complement of an embedded disc
giving by contracting the complement of an embedded disc 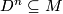 . At a point
. At a point 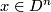 , this map is bijective and has local degree
, this map is bijective and has local degree 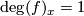 and so
and so 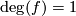 by the fact that the degree is the sum of local degrees, i.e.
by the fact that the degree is the sum of local degrees, i.e. 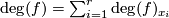 where
where 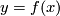 and
and 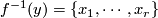 which in this case is just
which in this case is just 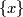 .
.
Now specialise to the case 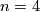 and
and 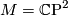 ,
, 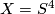 and consider
and consider 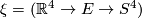 , an arbitrary 4-dimensional real vector bundle over
, an arbitrary 4-dimensional real vector bundle over 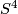 . If there is a normal map
. If there is a normal map 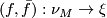 then, since this is a fibrewise isomorphism we must have that
then, since this is a fibrewise isomorphism we must have that 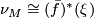 . Consider the first Pontryagin classes
. Consider the first Pontryagin classes 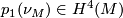 and
and 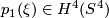 . With respect to some identifications
. With respect to some identifications 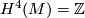 and
and 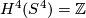 , we will show that
, we will show that 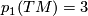 and
and 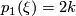 for some
for some 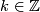 which will depend on the choice of bundle
which will depend on the choice of bundle  .
.
This would complete the proof since this would imply that 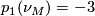 but also that
but also that 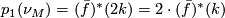 which is divisible by two. Note that that fact that
which is divisible by two. Note that that fact that 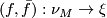 is only a stable bundle map is dealt with here by the fact that
is only a stable bundle map is dealt with here by the fact that 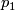 is a stable bundle invariant and so gives that same construction for any two stably isomorphic bundles of the same dimension.
is a stable bundle invariant and so gives that same construction for any two stably isomorphic bundles of the same dimension.
To show that 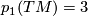 for
for 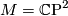 and some choice of identification
and some choice of identification 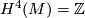 , we can use a number of techniques. One quick trick is to note that the Hirzebruch Signature Theorem applies to
, we can use a number of techniques. One quick trick is to note that the Hirzebruch Signature Theorem applies to  and gives that
and gives that ![\sigma(M) =\frac{1}{3} p_1(TM)[M]](/images/math/4/d/a/4da72ae5bd441a85e40dff8d6245227d.png) by the fact that the first polynomial is the multiplicative sequence corresponding to the
by the fact that the first polynomial is the multiplicative sequence corresponding to the  -genus is
-genus is 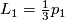 . Now
. Now 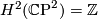 and the intersection form is
and the intersection form is 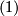 gives that
gives that 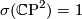 and so
and so ![p_1(TM)[M] =3](/images/math/4/9/7/497b22c8074202e4510529b77c6281f0.png) . Hence
. Hence 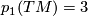 with appropriate identifications. Another, more elementary, method is to show that
with appropriate identifications. Another, more elementary, method is to show that 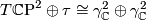 where
where 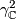 is the tautological complex line bundle over
is the tautological complex line bundle over 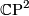 . This allows us to compute the total Chern class immediately which can then be used to recover the Pontryagin classes using the the highly useful formula
. This allows us to compute the total Chern class immediately which can then be used to recover the Pontryagin classes using the the highly useful formula 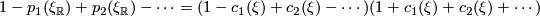 where
where 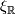 denotes that fibrewise replacement of
denotes that fibrewise replacement of 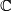 with
with 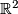 .
.
To show that 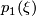 is always even is more tricky, and is asserted (but not proven) in Milnor's paper which proves the existence of exotic
is always even is more tricky, and is asserted (but not proven) in Milnor's paper which proves the existence of exotic  -spheres. Firstly let
-spheres. Firstly let 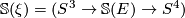 be the sphere bundle corresponding to
be the sphere bundle corresponding to  . Recall that, by clutching construction for bundles over spheres, there is a 1-1 correspondence between fibre bundles over
. Recall that, by clutching construction for bundles over spheres, there is a 1-1 correspondence between fibre bundles over  with fixed fibre
with fixed fibre  and structure group
and structure group  and
and 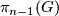 . Hence oriented
. Hence oriented  -bundles over
-bundles over 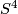 are classified by
are classified by 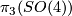 . One can show explicitly that
. One can show explicitly that 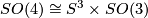 and so has universal cover
and so has universal cover 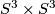 and therefore
and therefore 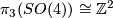 since covering maps induce isomorphisms on higher homotopy groups. Fix an explicit identification of
since covering maps induce isomorphisms on higher homotopy groups. Fix an explicit identification of 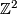 with
with 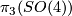 . Therefore
. Therefore 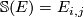 where
where 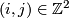 labels the element of
labels the element of 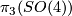 corresponding to the sphere bundle.
corresponding to the sphere bundle.
There is a map 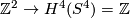 given by mapping
given by mapping 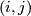 to
to 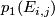 . By considering the inclusion of the fibre of the corresponding real vector bundle into the total space, one can show that this map factors as group homomorphisms
. By considering the inclusion of the fibre of the corresponding real vector bundle into the total space, one can show that this map factors as group homomorphisms 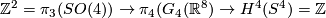 where
where 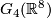 is the Grassmannian , i.e. the
is the Grassmannian , i.e. the  -dimensional linear subspaces of
-dimensional linear subspaces of 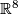 . Hence
. Hence 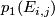 is linear in
is linear in  and
and  and so of the form
and so of the form 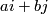 . By considering the quaternionic conjugate on the fibre, we can also show that
. By considering the quaternionic conjugate on the fibre, we can also show that 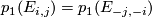 which guarantees that
which guarantees that 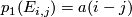 for some
for some 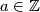 and some identification
and some identification 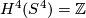 . To finish, we can check that
. To finish, we can check that 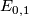 is the tautological bundle over
is the tautological bundle over 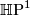 by using an explicit identification of
by using an explicit identification of 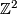 with
with 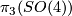 . This shows that
. This shows that 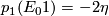 where
where 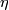 is the pullback of the chosen generator of
is the pullback of the chosen generator of 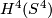 along an identification
along an identification 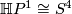 . This shows that
. This shows that 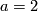 and hence
and hence 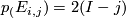 which completes the proof.
which completes the proof.
See also Obstruction classes and Pontrjagin classes (Ex).
2) For any  , let
, let 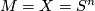 . Note that the stable normal bundle
. Note that the stable normal bundle 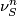 is trivial since the normal bundle of the codimension one embedding
is trivial since the normal bundle of the codimension one embedding 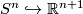 is trivial. Hence any map
is trivial. Hence any map 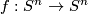 extends to a bundle map
extends to a bundle map 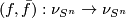 and so it suffices to find degree
and so it suffices to find degree  maps
maps 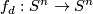 for any
for any  .
.
For  , a degree
, a degree  map
map 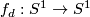 is given by wrapping the circle
is given by wrapping the circle  times around itself. By suspending
times around itself. By suspending  times we get a map
times we get a map 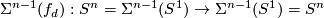 which we can show still has degree
which we can show still has degree  by using local degrees as in the previous exercise.
by using local degrees as in the previous exercise.
3) We will show that there is a degree one normal map 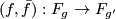 if and only if
if and only if 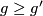 . Firstly note that, as above, the codimension one embedding
. Firstly note that, as above, the codimension one embedding 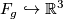 is trivial and so
is trivial and so 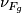 is trivial for all
is trivial for all  . Hence any map extends to a normal map and it remains to show that there is a degree one map
. Hence any map extends to a normal map and it remains to show that there is a degree one map 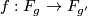 if and only if
if and only if 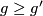 .
.
If 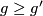 , then we can get a map
, then we can get a map 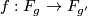 by contracting the complement of the standard
by contracting the complement of the standard 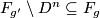 . This is degree one using local degree as in the first exercise.
. This is degree one using local degree as in the first exercise.
Let 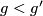 and suppose there is a map
and suppose there is a map 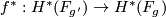 of cohomology rings sending the generator of
of cohomology rings sending the generator of 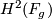 to the generator of
to the generator of 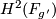 . Note that
. Note that 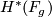 is generated by
is generated by 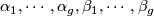 in degree one and
in degree one and 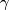 is degree two such that
is degree two such that 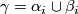 for
for 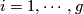 and all other products of the degree one generators zero. This can be lifted from the quotient map
and all other products of the degree one generators zero. This can be lifted from the quotient map 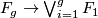 and the structure of the cohomology ring of
and the structure of the cohomology ring of 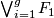 coming from that of
coming from that of 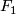 . Since
. Since 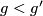 , the map
, the map 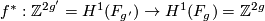 has a non-zero element
has a non-zero element 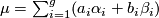 in its kernel. Suppose, without loss of generality, that
in its kernel. Suppose, without loss of generality, that 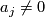 . Then
. Then 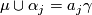 and so
and so 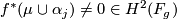 . However
. However 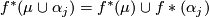 and
and 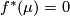 by hypothesis. This is a contradiction.
by hypothesis. This is a contradiction.
This can also be proven by using that a degree one map 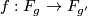 induces a surjection
induces a surjection 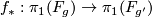 and so a surjection
and so a surjection 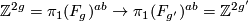 which gives a contradiction as before.
which gives a contradiction as before.