Talk:Normal bordism - definitions (Ex)
From Manifold Atlas
(Difference between revisions)
| Line 10: | Line 10: | ||
\mathcal{N}_n(X,k):= | \mathcal{N}_n(X,k):= | ||
\left\{ | \left\{ | ||
| − | (\xi,M,i,f,\overline{f}) \right\}/\ | + | (\xi,M,i,f,\overline{f}) \right\}/\sim$$ |
Here | Here | ||
# $\xi$ is a vector bundle of rank k over $X$, | # $\xi$ is a vector bundle of rank k over $X$, | ||
| Line 37: | Line 37: | ||
\mathcal{N}^T_n(X,k):= | \mathcal{N}^T_n(X,k):= | ||
\left\{ | \left\{ | ||
| − | (\xi,M,a,f,\overline{f}) \right\}/\ | + | (\xi,M,a,f,\overline{f}) \right\}/\sim $$ |
Here | Here | ||
# $\xi$ is a vector bundle of rank k over $X$, | # $\xi$ is a vector bundle of rank k over $X$, | ||
Latest revision as of 08:20, 3 April 2012
In both parts let 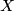 be a connected finite Poincare complex of dimension
be a connected finite Poincare complex of dimension 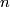 and let
and let 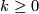 .
.
Part 1
The following definition of the set of normal maps 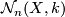 is similar to [Lück2001, Definition 3.46].
We define
is similar to [Lück2001, Definition 3.46].
We define
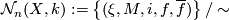
Here
-
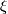 is a vector bundle of rank k over
is a vector bundle of rank k over 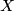 ,
,
-
 is a closed manifold of dimension n,
is a closed manifold of dimension n,
-
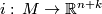 is an embedding,
is an embedding,
-
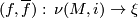 is a bundle map,
is a bundle map,
-
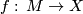 is of degree
is of degree 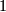 .
.
We identify 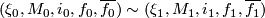 iff
iff
- There exists a compact manifold
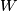 of dimension
of dimension 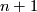 whose boundary can be written as
whose boundary can be written as 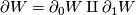 .
.
- There exists an embedding
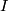 :
: ![W\to\mathbb{R}^{n+k}\times[0,1]](/images/math/a/b/1/ab18bc810bf5b65819b8394370060ae0.png) such that for
such that for 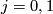 we have
we have 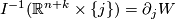 and
and 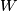 meets
meets 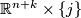 transversally.
transversally.
- There exists a vector bundle
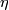 :
: ![E'\to X\times[0,1]](/images/math/8/6/f/86f9e8c19953967e1608f5175d2d4f00.png) of rank
of rank 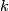 and for
and for 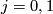 there exist vector bundle isomorphisms
there exist vector bundle isomorphisms 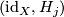 :
: 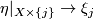 .
.
- There exists a bundle map
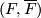 :
: 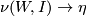 such that
such that
- for
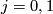 we have
we have 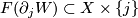
-
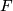 :
: ![(W,\partial W)\to(X\times[0,1],X\times\partial[0,1])](/images/math/1/9/5/19515ecbc55dfa41d99b7f8f412e4624.png) has degree one as a map between Poincare pairs.
has degree one as a map between Poincare pairs.
- for
- For
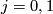 there exist diffeomorphisms
there exist diffeomorphisms 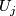 :
: 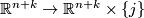 such that
such that
-
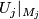 :
: 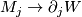 is a diffeomorphism
is a diffeomorphism
-
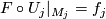
- the induced bundle map
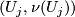 :
: 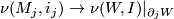 satisfies
satisfies 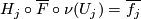 .
.
-
Part 2
The following definition of the set of tangential normal maps 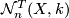 differs from [Lück2001, Definition 3.50].
We define
differs from [Lück2001, Definition 3.50].
We define
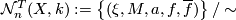
Here
-
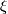 is a vector bundle of rank k over
is a vector bundle of rank k over 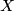 ,
,
-
 is a closed manifold of dimension n,
is a closed manifold of dimension n,
-
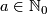 ,
,
-
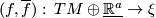 is a bundle map and
is a bundle map and
-
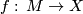 is degree 1.
is degree 1.
We identify 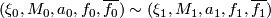 iff
iff
- There exists a compact manifold
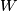 of dimension
of dimension 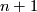 whose boundary can be written as
whose boundary can be written as 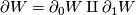 .
.
- There exists a vector bundle
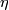 :
: ![E'\to X\times[0,1]](/images/math/8/6/f/86f9e8c19953967e1608f5175d2d4f00.png) and there exist
and there exist 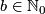 and a bundle map
and a bundle map 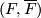 :
: 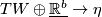 such that
such that
- for
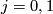 we have
we have 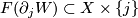
-
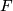 :
: ![(W,\partial W)\to(X\times[0,1],X\times\partial[0,1])](/images/math/1/9/5/19515ecbc55dfa41d99b7f8f412e4624.png) has degree one as a map between Poincare pairs.
has degree one as a map between Poincare pairs.
- for
- For
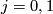 there exist diffeomorphisms
there exist diffeomorphisms 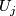 :
: 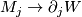 such that
such that 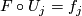 .
.
- For
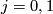 there exist bundle isomorphisms
there exist bundle isomorphisms 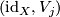 :
: 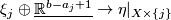 such that commutes. Here
such that commutes. Here![\displaystyle \xymatrix{TM_j\oplus\underline{\mathbb{R}}\oplus\underline{\mathbb{R}^b} \ar[rr]^{\overline{f_j}\oplus\mathrm{id}_{\underline{\mathbb{R}^{b-a_j+1}}}} \ar[d]_{TU_j\oplus n_j\oplus\mathrm{id}_{\underline{\mathbb{R}^b}}} & & \xi_j\oplus\underline{\mathbb{R}^{b-a_j+1}} \ar[d]^{V_j}\\ TW|_{\partial_jW}\oplus\underline{\mathbb{R}^b} \ar[rr]^{\overline{F}|_{\partial_jW}} & & \eta|_{X\times\{j\}} }](/images/math/7/4/e/74e20705c840b6ca855d5ac331779b90.png)
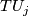 :
: 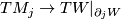 is the differential of
is the differential of 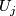 and
and 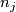 :
: 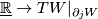 is given by an inward normal field of
is given by an inward normal field of 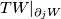 .
.
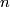 and let
and let 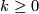 .
.
Part 1
The following definition of the set of normal maps 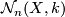 is similar to [Lück2001, Definition 3.46].
We define
is similar to [Lück2001, Definition 3.46].
We define
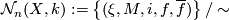
Here
-
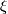 is a vector bundle of rank k over
is a vector bundle of rank k over 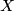 ,
,
-
 is a closed manifold of dimension n,
is a closed manifold of dimension n,
-
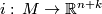 is an embedding,
is an embedding,
-
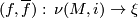 is a bundle map,
is a bundle map,
-
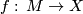 is of degree
is of degree 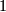 .
.
We identify 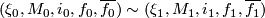 iff
iff
- There exists a compact manifold
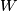 of dimension
of dimension 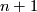 whose boundary can be written as
whose boundary can be written as 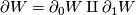 .
.
- There exists an embedding
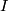 :
: ![W\to\mathbb{R}^{n+k}\times[0,1]](/images/math/a/b/1/ab18bc810bf5b65819b8394370060ae0.png) such that for
such that for 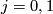 we have
we have 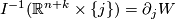 and
and 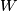 meets
meets 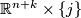 transversally.
transversally.
- There exists a vector bundle
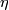 :
: ![E'\to X\times[0,1]](/images/math/8/6/f/86f9e8c19953967e1608f5175d2d4f00.png) of rank
of rank 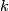 and for
and for 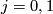 there exist vector bundle isomorphisms
there exist vector bundle isomorphisms 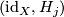 :
: 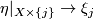 .
.
- There exists a bundle map
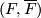 :
: 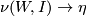 such that
such that
- for
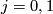 we have
we have 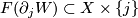
-
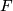 :
: ![(W,\partial W)\to(X\times[0,1],X\times\partial[0,1])](/images/math/1/9/5/19515ecbc55dfa41d99b7f8f412e4624.png) has degree one as a map between Poincare pairs.
has degree one as a map between Poincare pairs.
- for
- For
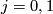 there exist diffeomorphisms
there exist diffeomorphisms 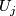 :
: 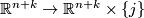 such that
such that
-
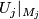 :
: 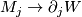 is a diffeomorphism
is a diffeomorphism
-
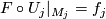
- the induced bundle map
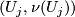 :
: 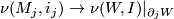 satisfies
satisfies 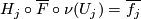 .
.
-
Part 2
The following definition of the set of tangential normal maps 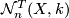 differs from [Lück2001, Definition 3.50].
We define
differs from [Lück2001, Definition 3.50].
We define
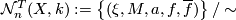
Here
-
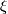 is a vector bundle of rank k over
is a vector bundle of rank k over 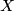 ,
,
-
 is a closed manifold of dimension n,
is a closed manifold of dimension n,
-
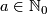 ,
,
-
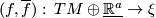 is a bundle map and
is a bundle map and
-
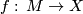 is degree 1.
is degree 1.
We identify 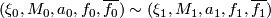 iff
iff
- There exists a compact manifold
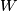 of dimension
of dimension 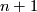 whose boundary can be written as
whose boundary can be written as 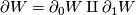 .
.
- There exists a vector bundle
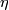 :
: ![E'\to X\times[0,1]](/images/math/8/6/f/86f9e8c19953967e1608f5175d2d4f00.png) and there exist
and there exist 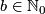 and a bundle map
and a bundle map 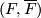 :
: 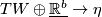 such that
such that
- for
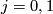 we have
we have 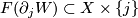
-
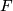 :
: ![(W,\partial W)\to(X\times[0,1],X\times\partial[0,1])](/images/math/1/9/5/19515ecbc55dfa41d99b7f8f412e4624.png) has degree one as a map between Poincare pairs.
has degree one as a map between Poincare pairs.
- for
- For
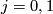 there exist diffeomorphisms
there exist diffeomorphisms 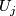 :
: 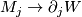 such that
such that 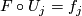 .
.
- For
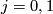 there exist bundle isomorphisms
there exist bundle isomorphisms 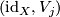 :
: 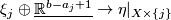 such that commutes. Here
such that commutes. Here![\displaystyle \xymatrix{TM_j\oplus\underline{\mathbb{R}}\oplus\underline{\mathbb{R}^b} \ar[rr]^{\overline{f_j}\oplus\mathrm{id}_{\underline{\mathbb{R}^{b-a_j+1}}}} \ar[d]_{TU_j\oplus n_j\oplus\mathrm{id}_{\underline{\mathbb{R}^b}}} & & \xi_j\oplus\underline{\mathbb{R}^{b-a_j+1}} \ar[d]^{V_j}\\ TW|_{\partial_jW}\oplus\underline{\mathbb{R}^b} \ar[rr]^{\overline{F}|_{\partial_jW}} & & \eta|_{X\times\{j\}} }](/images/math/7/4/e/74e20705c840b6ca855d5ac331779b90.png)
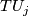 :
: 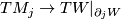 is the differential of
is the differential of 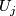 and
and 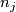 :
: 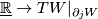 is given by an inward normal field of
is given by an inward normal field of 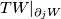 .
.