Talk:Normal bordism - definitions (Ex)
| Line 22: | Line 22: | ||
where we identify $(\xi_0,M_0,i_0,f_0,\overline{f_0})\sim(\xi_1,M_1,i_1,f_1,\overline{f_1})$ iff | where we identify $(\xi_0,M_0,i_0,f_0,\overline{f_0})\sim(\xi_1,M_1,i_1,f_1,\overline{f_1})$ iff | ||
| − | 1) | + | 1) There exists a compact manifold $W$ of dimension $n+1$ whose boundary can be written as $\partial W=\partial_0W\amalg\partial_1W$. |
| − | 2) | + | 2) There exists an embedding $I$: $W\to\mathbb{R}^{n+k}\times[0,1]$ such that for $j=0,1$ we have |
| − | $I^{-1}(\mathbb{R}^{n+k}\times\{j\})=\partial_jW$ and $W$ meets $\mathbb{R}^{n+k}\times\{j\}$ transversally | + | $I^{-1}(\mathbb{R}^{n+k}\times\{j\})=\partial_jW$ and $W$ meets $\mathbb{R}^{n+k}\times\{j\}$ transversally. |
| − | 3) | + | 3) There exists a vector bundle $\eta$: $E'\to X\times[0,1]$ of rank $k$ |
| − | and for $j=0,1$ there exist vector bundle isomorphisms $(\mathrm{id}_X,H_j)$: $\eta|_{X\times\{j\}}\to\xi_j$ | + | and for $j=0,1$ there exist vector bundle isomorphisms $(\mathrm{id}_X,H_j)$: $\eta|_{X\times\{j\}}\to\xi_j$. |
| − | 4) | + | 4) There exists a bundle map $(F,\overline{F})$: $\nu(W,I)\to\eta$ such that for $j=0,1$ we have $F(\partial_jW)\subset X\times\{j\}$ |
and such that $F$: $(W,\partial W)\to(X\times[0,1],X\times\partial[0,1])$ | and such that $F$: $(W,\partial W)\to(X\times[0,1],X\times\partial[0,1])$ | ||
has degree one as a map between Poincare pairs. | has degree one as a map between Poincare pairs. | ||
| − | 5) | + | 5) For $j=0,1$ there exist diffeomorphisms $U_j$: $\mathbb{R}^{n+k}\to\mathbb{R}^{n+k}\times\{j\}$ such that |
a) $U_j|_{M_j}$: $M_j\to\partial_jW$ is a diffeomorphism | a) $U_j|_{M_j}$: $M_j\to\partial_jW$ is a diffeomorphism | ||
| Line 59: | Line 59: | ||
\right\} | \right\} | ||
$$ | $$ | ||
| + | where we identify $(\xi_0,M_0,a_0,f_0,\overline{f_0})\sim(\xi_1,M_1,a_1,f_1,\overline{f_1})$ iff | ||
| + | |||
| + | 1) There exists a compact manifold $W$ of dimension $n+1$ whose boundary can be written as $\partial W=\partial_0W\amalg\partial_1W$. | ||
| + | |||
| + | 2) There exists a vector bundle $\eta$: $E'\to X\times[0,1]$ and there exist $b\in\mathbb{N}_0$ and | ||
| + | a bundle map $(F,\overline{F})$: $TW\oplus\underline{\mathbb{R}^b}\to\eta$ | ||
| + | such that for $j=0,1$ we have $F(\partial_jW)\subset X\times\{j\}$ | ||
| + | and such that $F$: $(W,\partial W)\to(X\times[0,1],X\times\partial[0,1])$ | ||
| + | has degree one as a map between Poincare pairs. | ||
| + | |||
| + | 3) For $j=0,1$ there exist diffeomorphisms $U_j$: $M_j\to\partial_jW$ such that $F\circ U_j=f_j$. | ||
| + | |||
| + | 4) For $j=0,1$ there exist bundle isomorphisms $(\mathrm{id}_X,V_j)$: $\xi_j\oplus\underline{\mathbb{R}^{b-a_j+1}}\to\eta|_{X\times\{j\}}$ | ||
| + | such that $V_j\circ(\overline{f_j}\oplus\mathrm{id}_{\underline{\mathbb{R}^{b-a_j+1}}})=\overline{F}|_{\partial_jW}\circ(TU_j\oplus n_j\oplus\mathrm{id}_{\underline{\mathbb{R}^b}})$. | ||
| + | Here $TU_j$: $TM_j\to TW|_{\partial_jW}$ is the differential of $U_j$ and $n_j$: $\underline{\mathbb{R}}\to TW|_{\partial_jW}$ is given by an inward normal field of $TW|_{\partial_jW}$. | ||
</wikitex> | </wikitex> | ||
Revision as of 11:44, 2 April 2012
In both parts let  be a connected finite Poincare complex of dimension
be a connected finite Poincare complex of dimension  and let
and let 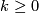 .
.
Part 1
The following definition of the set of normal maps 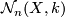 is similar to [Lück2001, Definition 3.46].
We define
is similar to [Lück2001, Definition 3.46].
We define
![\displaystyle \mathcal{N}_n(X,k):= \left\{ [\xi,M,i,f,\overline{f}] | \begin{array}{l} \xi\textrm{ vector bundle of rank }k\textrm{ over }X,\, M\textrm{ closed manifold of dimension }n,\, i:\,M\to\mathbb{R}^{n+k}\textrm{ embedding},\, (f,\overline{f}):\,\nu(M,i)\to\xi\textrm{ bundle map},\, f\textrm{ of degree }1 \end{array} \right\}](/images/math/3/8/9/38962ae773ef41b834b8be2c52e0655e.png)
where we identify 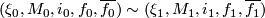 iff
iff
1) There exists a compact manifold  of dimension
of dimension 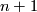 whose boundary can be written as
whose boundary can be written as 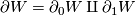 .
.
2) There exists an embedding  :
: ![W\to\mathbb{R}^{n+k}\times[0,1]](/images/math/a/b/1/ab18bc810bf5b65819b8394370060ae0.png) such that for
such that for 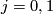 we have
we have
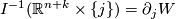 and
and  meets
meets 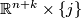 transversally.
transversally.
3) There exists a vector bundle 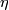 :
: ![E'\to X\times[0,1]](/images/math/8/6/f/86f9e8c19953967e1608f5175d2d4f00.png) of rank
of rank  and for
and for 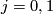 there exist vector bundle isomorphisms
there exist vector bundle isomorphisms 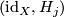 :
: 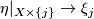 .
.
4) There exists a bundle map 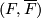 :
: 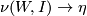 such that for
such that for 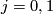 we have
we have 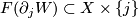 and such that
and such that  :
: ![(W,\partial W)\to(X\times[0,1],X\times\partial[0,1])](/images/math/1/9/5/19515ecbc55dfa41d99b7f8f412e4624.png) has degree one as a map between Poincare pairs.
has degree one as a map between Poincare pairs.
5) For 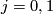 there exist diffeomorphisms
there exist diffeomorphisms 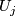 :
: 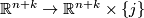 such that
such that
a) 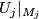 :
: 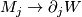 is a diffeomorphism
is a diffeomorphism
b) 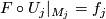
c) the induced bundle map 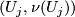 :
: 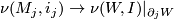 satisfies
satisfies 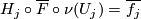 .
.
Part 2
The following definition of the set of tangential normal maps 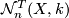 differs from [Lück2001, Definition 3.50].
We define
differs from [Lück2001, Definition 3.50].
We define
![\displaystyle \mathcal{N}^T_n(X,k):= \left\{ [\xi,M,a,f,\overline{f}] | \begin{array}{l} \xi\textrm{ vector bundle of rank }k\textrm{ over }X,\, M\textrm{ closed manifold of dimension }n,\, a\in\mathbb{N}_0,\, (f,\overline{f}):\,TM\oplus\underline{\mathbb{R}^a}\to\xi\textrm{ bundle map},\, f\textrm{ of degree }1 \end{array} \right\}](/images/math/e/3/0/e3035e82586359a6866457cc57b3f496.png)
where we identify 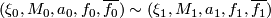 iff
iff
1) There exists a compact manifold  of dimension
of dimension 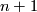 whose boundary can be written as
whose boundary can be written as 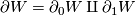 .
.
2) There exists a vector bundle 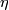 :
: ![E'\to X\times[0,1]](/images/math/8/6/f/86f9e8c19953967e1608f5175d2d4f00.png) and there exist
and there exist 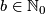 and
a bundle map
and
a bundle map 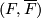 :
: 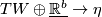 such that for
such that for 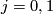 we have
we have 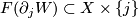 and such that
and such that  :
: ![(W,\partial W)\to(X\times[0,1],X\times\partial[0,1])](/images/math/1/9/5/19515ecbc55dfa41d99b7f8f412e4624.png) has degree one as a map between Poincare pairs.
has degree one as a map between Poincare pairs.
3) For 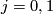 there exist diffeomorphisms
there exist diffeomorphisms 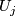 :
: 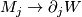 such that
such that 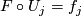 .
.
4) For 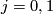 there exist bundle isomorphisms
there exist bundle isomorphisms 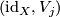 :
: 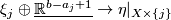 such that
such that 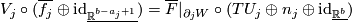 .
Here
.
Here 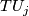 :
: 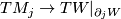 is the differential of
is the differential of 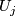 and
and 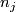 :
: 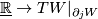 is given by an inward normal field of
is given by an inward normal field of 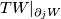 .
.