Talk:Non-prime solvable fundamental groups (Ex)
Suggestion: The first manifold is 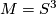 . Other than that, non-prime manifolds possess prime decompositions. So there must be at least two manifolds connected sum to each other. The fundamental group of
. Other than that, non-prime manifolds possess prime decompositions. So there must be at least two manifolds connected sum to each other. The fundamental group of  is the free product of the fundamental groups of the various fundamental groups. Since it's solvable, note that each abelian quotient group can only contain elements from any individual fundamental group, otherwise it wouldn't be abelian. Suppose at least two fundamental groups of the component manifolds
is the free product of the fundamental groups of the various fundamental groups. Since it's solvable, note that each abelian quotient group can only contain elements from any individual fundamental group, otherwise it wouldn't be abelian. Suppose at least two fundamental groups of the component manifolds 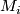 are nontrivial. Consider the first time in the series
are nontrivial. Consider the first time in the series 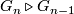 such that
such that 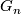 contains a nontrivial element
contains a nontrivial element  from some
from some 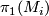 , where no element from
, where no element from 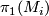 appears in
appears in 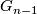 .
. 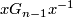 is a contradiction to normality, since they are in a free product. If there's only one component
is a contradiction to normality, since they are in a free product. If there's only one component  with nontrivial fundamental group, then use the Hurewicz theorem to control the homology of the remaining components.
with nontrivial fundamental group, then use the Hurewicz theorem to control the homology of the remaining components.