Talk:Non-prime solvable fundamental groups (Ex)

1 Suggestion

The first manifold is 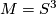$M = S^3$$\newcommand{\Z}{\mathbb{Z}} \newcommand{\R}{\mathbb{R}} \newcommand{\C}{\mathbb{C}} \newcommand{\N}{\mathbb{N}} \newcommand{\Q}{\mathbb{Q}} \newcommand{\F}{\mathbb{F}} \newcommand{\bZ}{\mathbb{Z}} \newcommand{\bR}{\mathbb{R}} \newcommand{\bC}{\mathbb{C}} \newcommand{\bH}{\mathbb{H}} \newcommand{\bQ}{\mathbb{Q}} \newcommand{\bF}{\mathbb{F}} \newcommand{\bN}{\mathbb{N}} \DeclareMathOperator\id{id} % identity map \DeclareMathOperator\Sq{Sq} % Steenrod squares \DeclareMathOperator\Homeo{Homeo} % group of homeomorphisms of a topoloical space \DeclareMathOperator\Diff{Diff} % group of diffeomorphisms of a smooth manifold \DeclareMathOperator\SDiff{SDiff} % diffeomorphism under some constraint \DeclareMathOperator\Hom{Hom} % homomrphism group \DeclareMathOperator\End{End} % endomorphism group \DeclareMathOperator\Aut{Aut} % automorphism group \DeclareMathOperator\Inn{Inn} % inner automorphisms \DeclareMathOperator\Out{Out} % outer automorphism group \DeclareMathOperator\vol{vol} % volume \newcommand{\GL}{\text{GL}} % general linear group \newcommand{\SL}{\text{SL}} % special linear group \newcommand{\SO}{\text{SO}} % special orthogonal group \newcommand{\O}{\text{O}} % orthogonal group \newcommand{\SU}{\text{SU}} % special unitary group \newcommand{\Spin}{\text{Spin}} % Spin group \newcommand{\RP}{\Rr\mathrm P} % real projective space \newcommand{\CP}{\Cc\mathrm P} % complex projective space \newcommand{\HP}{\Hh\mathrm P} % quaternionic projective space \newcommand{\Top}{\mathrm{Top}} % topological category \newcommand{\PL}{\mathrm{PL}} % piecewise linear category \newcommand{\Cat}{\mathrm{Cat}} % any category \newcommand{\KS}{\text{KS}} % Kirby-Siebenmann class \newcommand{\Hud}{\text{Hud}} % Hudson torus \newcommand{\Ker}{\text{Ker}} % Kernel \newcommand{\underbar}{\underline} %Classifying Spaces for Families of Subgroups \newcommand{\textup}{\text} \newcommand{\sp}{^}M = S^3$. Other than that, non-prime manifolds possess prime decompositions. So there must be at least two manifolds connected sum to each other. The fundamental group of $M$$M$ is the free product of the fundamental groups of the various fundamental groups. Since it's solvable, note that each abelian quotient group can only contain elements from any individual fundamental group, otherwise it wouldn't be abelian. 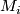Suppose at least two fundamental groups of the component manifolds $M_i$$M_i$ are nontrivial. 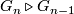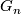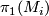Consider the first time in the series $G_n \triangleright G_{n-1}$$G_n \triangleright G_{n-1}$ such that $G_n$$G_n$ contains a nontrivial element $x$$x$ from some $\pi_1(M_i)$$\pi_1(M_i)$, where no element from 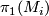$\pi_1(M_i)$$\pi_1(M_i)$ appears in 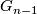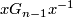$G_{n-1}$$G_{n-1}$. $xG_{n-1}x^{-1}$$xG_{n-1}x^{-1}$ is a contradiction to normality, since they are in a free product. If there's only one component $M_1$$M_1$ with nontrivial fundamental group, then use the Hurewicz theorem to control the homology of the remaining components.

2 Solution

Suppose that $M$$M$ is an orientable closed 3-manifold that is not prime, i.e., it splits as a connected sum 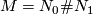$M=N_0\#N_1$$M=N_0\#N_1$ of two orientable closed 3-manifolds with non-trivial fundamental groups. Then 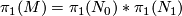$\pi_1(M)=\pi_1(N_0)\ast\pi_1(N_1)$$\pi_1(M)=\pi_1(N_0)\ast\pi_1(N_1)$. But a free product of two non-trivial groups contains a free group, and is thus not solvable, unless both factors are 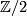$\mathbb{Z}/2$$\mathbb{Z}/2$. 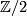It follows that $M$$M$ must be a connected sum of two (prime) orientable closed 3-manifolds with fundamental groups equal to $\mathbb{Z}/2$$\mathbb{Z}/2$, and any such sum actually has the desired property.

We will now show that the only such example is given by the connected sum 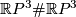$\mathbb{R}P^3\#\mathbb{R}P^3$$\mathbb{R}P^3\#\mathbb{R}P^3$. In order to see this we need to show that any prime orientable closed 3-manifold with fundamental group isomorphic to 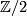$\mathbb{Z}/2$$\mathbb{Z}/2$ is already homeomorphic to 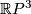$\mathbb{R}P^3$$\mathbb{R}P^3$. By the Geometrization Conjecture, such a manifold has universal covering homeomorphic to $S^3$$S^3$ and the action on the universal covering is conjugate by homeomorphisms to the action of an order 2 subgroup of $SO(4)$$SO(4)$ on $S^3$$S^3$. 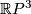But all such subgroups that act freely on $S^3$$S^3$ are conjugate to the one where the non-trivial element acts via the antipodal map, and thus yield $\mathbb{R}P^3$$\mathbb{R}P^3$ as the quotient.