Talk:Non-prime solvable fundamental groups (Ex)
| Line 3: | Line 3: | ||
The first manifold is $M = S^3$. Other than that, non-prime manifolds possess prime decompositions. So there must be at least two manifolds connected sum to each other. The fundamental group of $M$ is the free product of the fundamental groups of the various fundamental groups. Since it's solvable, note that each abelian quotient group can only contain elements from any individual fundamental group, otherwise it wouldn't be abelian. Suppose at least two fundamental groups of the component manifolds $M_i$ are nontrivial. Consider the first time in the series $G_n \triangleright G_{n-1}$ such that $G_n$ contains a nontrivial element $x$ from some $\pi_1(M_i)$, where no element from $\pi_1(M_i)$ appears in $G_{n-1}$. $xG_{n-1}x^{-1}$ is a contradiction to normality, since they are in a free product. If there's only one component $M_1$ with nontrivial fundamental group, then use the Hurewicz theorem to control the homology of the remaining components. | The first manifold is $M = S^3$. Other than that, non-prime manifolds possess prime decompositions. So there must be at least two manifolds connected sum to each other. The fundamental group of $M$ is the free product of the fundamental groups of the various fundamental groups. Since it's solvable, note that each abelian quotient group can only contain elements from any individual fundamental group, otherwise it wouldn't be abelian. Suppose at least two fundamental groups of the component manifolds $M_i$ are nontrivial. Consider the first time in the series $G_n \triangleright G_{n-1}$ such that $G_n$ contains a nontrivial element $x$ from some $\pi_1(M_i)$, where no element from $\pi_1(M_i)$ appears in $G_{n-1}$. $xG_{n-1}x^{-1}$ is a contradiction to normality, since they are in a free product. If there's only one component $M_1$ with nontrivial fundamental group, then use the Hurewicz theorem to control the homology of the remaining components. | ||
| − | == | + | == Solution == |
Suppose that $M$ is an orientable closed 3-manifold that is not prime, i.e., it splits as a connected sum $M=N_0\#N_1$ of two orientable closed 3-manifolds with non-trivial fundamental groups. Then $\pi_1(M)=\pi_1(N_0)\ast\pi_1(N_1)$. But a free product of two non-trivial groups contains a free group, and is thus not solvable, unless both factors are $\mathbb{Z}/2$. It follows that $M$ must be a connected sum of two (prime) orientable closed 3-manifolds with fundamental groups equal to $\mathbb{Z}/2$, and any such sum actually has the desired property. | Suppose that $M$ is an orientable closed 3-manifold that is not prime, i.e., it splits as a connected sum $M=N_0\#N_1$ of two orientable closed 3-manifolds with non-trivial fundamental groups. Then $\pi_1(M)=\pi_1(N_0)\ast\pi_1(N_1)$. But a free product of two non-trivial groups contains a free group, and is thus not solvable, unless both factors are $\mathbb{Z}/2$. It follows that $M$ must be a connected sum of two (prime) orientable closed 3-manifolds with fundamental groups equal to $\mathbb{Z}/2$, and any such sum actually has the desired property. | ||
We will now show that the only such example is given by the connected sum $\mathbb{R}P^3\#\mathbb{R}P^3$. In order to see this we need to show that any prime orientable closed 3-manifold with fundamental group isomorphic to $\mathbb{Z}/2$ is already homeomorphic to $\mathbb{R}P^3$. By the Geometrization Conjecture, such a manifold has universal covering homeomorphic to $S^3$ and the action on the universal covering is conjugate by homeomorphisms to the action of an order 2 subgroup of $SO(4)$ on $S^3$. But all these subgroups are conjugate to the one where the non-trivial element acts via the antipodal map, and thus yield $\mathbb{R}P^3$ as the quotient. | We will now show that the only such example is given by the connected sum $\mathbb{R}P^3\#\mathbb{R}P^3$. In order to see this we need to show that any prime orientable closed 3-manifold with fundamental group isomorphic to $\mathbb{Z}/2$ is already homeomorphic to $\mathbb{R}P^3$. By the Geometrization Conjecture, such a manifold has universal covering homeomorphic to $S^3$ and the action on the universal covering is conjugate by homeomorphisms to the action of an order 2 subgroup of $SO(4)$ on $S^3$. But all these subgroups are conjugate to the one where the non-trivial element acts via the antipodal map, and thus yield $\mathbb{R}P^3$ as the quotient. | ||
</wikitex> | </wikitex> | ||
Revision as of 00:21, 10 January 2019
1 Suggestion
The first manifold is 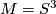 . Other than that, non-prime manifolds possess prime decompositions. So there must be at least two manifolds connected sum to each other. The fundamental group of
. Other than that, non-prime manifolds possess prime decompositions. So there must be at least two manifolds connected sum to each other. The fundamental group of  is the free product of the fundamental groups of the various fundamental groups. Since it's solvable, note that each abelian quotient group can only contain elements from any individual fundamental group, otherwise it wouldn't be abelian. Suppose at least two fundamental groups of the component manifolds
is the free product of the fundamental groups of the various fundamental groups. Since it's solvable, note that each abelian quotient group can only contain elements from any individual fundamental group, otherwise it wouldn't be abelian. Suppose at least two fundamental groups of the component manifolds 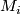 are nontrivial. Consider the first time in the series
are nontrivial. Consider the first time in the series 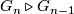 such that
such that 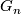 contains a nontrivial element
contains a nontrivial element  from some
from some 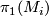 , where no element from
, where no element from 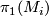 appears in
appears in 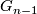 .
. 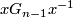 is a contradiction to normality, since they are in a free product. If there's only one component
is a contradiction to normality, since they are in a free product. If there's only one component  with nontrivial fundamental group, then use the Hurewicz theorem to control the homology of the remaining components.
with nontrivial fundamental group, then use the Hurewicz theorem to control the homology of the remaining components.
2 Solution
Suppose that  is an orientable closed 3-manifold that is not prime, i.e., it splits as a connected sum
is an orientable closed 3-manifold that is not prime, i.e., it splits as a connected sum 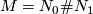 of two orientable closed 3-manifolds with non-trivial fundamental groups. Then
of two orientable closed 3-manifolds with non-trivial fundamental groups. Then 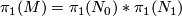 . But a free product of two non-trivial groups contains a free group, and is thus not solvable, unless both factors are
. But a free product of two non-trivial groups contains a free group, and is thus not solvable, unless both factors are 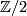 . It follows that
. It follows that  must be a connected sum of two (prime) orientable closed 3-manifolds with fundamental groups equal to
must be a connected sum of two (prime) orientable closed 3-manifolds with fundamental groups equal to 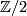 , and any such sum actually has the desired property.
, and any such sum actually has the desired property.
We will now show that the only such example is given by the connected sum 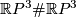 . In order to see this we need to show that any prime orientable closed 3-manifold with fundamental group isomorphic to
. In order to see this we need to show that any prime orientable closed 3-manifold with fundamental group isomorphic to 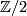 is already homeomorphic to
is already homeomorphic to 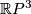 . By the Geometrization Conjecture, such a manifold has universal covering homeomorphic to
. By the Geometrization Conjecture, such a manifold has universal covering homeomorphic to  and the action on the universal covering is conjugate by homeomorphisms to the action of an order 2 subgroup of
and the action on the universal covering is conjugate by homeomorphisms to the action of an order 2 subgroup of  on
on  . But all these subgroups are conjugate to the one where the non-trivial element acts via the antipodal map, and thus yield
. But all these subgroups are conjugate to the one where the non-trivial element acts via the antipodal map, and thus yield 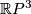 as the quotient.
as the quotient.