Talk:Middle-dimensional surgery kernel (Ex)
(Difference between revisions)
| Line 7: | Line 7: | ||
Note that $\ker(d_n) \subseteq C_n$ is a direct summand iff the sequence | Note that $\ker(d_n) \subseteq C_n$ is a direct summand iff the sequence | ||
$$ 0 \longrightarrow \ker(d_n) \longrightarrow C_n \stackrel{d_n}{\longrightarrow} \text{im}(d_n) \longrightarrow 0$$ | $$ 0 \longrightarrow \ker(d_n) \longrightarrow C_n \stackrel{d_n}{\longrightarrow} \text{im}(d_n) \longrightarrow 0$$ | ||
| − | splits. By exactness at $n-1$ however, we have $\text{im}(d_n) = \ker(d_{n-1})$ which is projective being a direct summand of a projective module. | + | splits. By exactness at $n-1$ however, we have $\text{im}(d_n) = \ker(d_{n-1})$ which is projective, being a direct summand of a projective module. |
| − | ad(1): Iterating the lemma we find that $\ker(d_n)$ is a direct summand of $C_n$ if the same statement holds for some lower $n$. However eventually both terms are zero, since the complex is finite. Being a direct summand in a finitely generated module $\ker(d_n)$ is then itself finitely generated, and hence also $H_n(C)$. The second assertion follows immediately from the universal coefficient theorem. | + | ad(1): Iterating the lemma we find that $\ker(d_n)$ is a direct summand of $C_n$ if the same statement holds for some lower $n$. However, eventually both terms are zero, since the complex is finite. Being a direct summand in a finitely generated module $\ker(d_n)$ is then itself finitely generated, and hence also $H_n(C)$. The second assertion follows immediately from the universal coefficient theorem. |
</wikitex> | </wikitex> | ||
Revision as of 12:22, 3 April 2012
First a little lemma:
Let 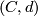 be a chain complex with
be a chain complex with 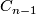 projective,
projective, 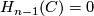 and
and 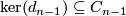 a direct summand. Then also
a direct summand. Then also 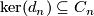 is a direct summand.
is a direct summand.
Proof:
Note that 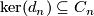 is a direct summand iff the sequence
is a direct summand iff the sequence
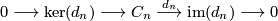
splits. By exactness at 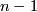 however, we have
however, we have 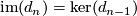 which is projective, being a direct summand of a projective module.
which is projective, being a direct summand of a projective module.
ad(1): Iterating the lemma we find that 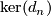 is a direct summand of
is a direct summand of 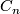 if the same statement holds for some lower
if the same statement holds for some lower  . However, eventually both terms are zero, since the complex is finite. Being a direct summand in a finitely generated module
. However, eventually both terms are zero, since the complex is finite. Being a direct summand in a finitely generated module 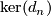 is then itself finitely generated, and hence also
is then itself finitely generated, and hence also 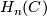 . The second assertion follows immediately from the universal coefficient theorem.
. The second assertion follows immediately from the universal coefficient theorem.