Talk:Middle-dimensional surgery kernel (Ex)
(Difference between revisions)
(Created page with "<wikitex> First a little lemma: Let $(C,d)$ be a chain complex with $C_{n-1}$ projective, $H_{n-1}(C) = 0$ and $\ker(d_{n-1}) \subseteq C_{n-1}$ a direct summand. Then also...") |
|||
| Line 1: | Line 1: | ||
<wikitex> | <wikitex> | ||
| − | First a little lemma: | + | First a little lemma: \\ |
| − | Let $(C,d)$ be a chain complex with $C_{n-1}$ projective, $H_{n-1}(C) = 0$ and $\ker(d_{n-1}) \subseteq C_{n-1}$ a direct summand. Then also $\ker(d_n) \subseteq C_n$ is a direct summand. | + | Let $(C,d)$ be a chain complex with $C_{n-1}$ projective, $H_{n-1}(C) = 0$ and $\ker(d_{n-1}) \subseteq C_{n-1}$ a direct summand. Then also $\ker(d_n) \subseteq C_n$ is a direct summand. \\ |
Proof: | Proof: | ||
Note that $\ker(d_n) \subseteq C_n$ is a direct summand iff the sequence | Note that $\ker(d_n) \subseteq C_n$ is a direct summand iff the sequence | ||
Revision as of 12:20, 3 April 2012
First a little lemma: \\
Let 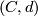 be a chain complex with
be a chain complex with 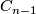 projective,
projective, 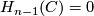 and
and 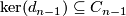 a direct summand. Then also
a direct summand. Then also 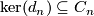 is a direct summand. \\
Proof:
Note that
is a direct summand. \\
Proof:
Note that 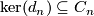 is a direct summand iff the sequence
is a direct summand iff the sequence
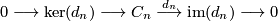
splits. By exactness at  however, we have
however, we have 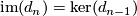 which is projective being a direct summand of a projective module.
which is projective being a direct summand of a projective module.
ad(1): Iterating the lemma we find that 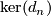 is a direct summand of
is a direct summand of 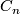 if the same statement holds for some lower
if the same statement holds for some lower  . However eventually both terms are zero, since the complex is finite. Being a direct summand in a finitely generated module
. However eventually both terms are zero, since the complex is finite. Being a direct summand in a finitely generated module 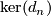 is then itself finitely generated, and hence also
is then itself finitely generated, and hence also 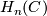 . The second assertion follows immediately from the universal coefficient theorem.
. The second assertion follows immediately from the universal coefficient theorem.