Talk:Idempotents in group rings (Ex)
Recall that by the representation theory of finite groups we have
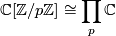
since all irreducibles are  -dimensional as the group is abelian. Hence the idempotents of
-dimensional as the group is abelian. Hence the idempotents of 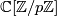 are precisely
are precisely  -tupels with entries either
-tupels with entries either  or
or  , since
, since 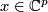 fulfills
fulfills 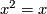 if and only if each
if and only if each 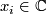 fulfills
fulfills 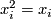 which implies the claim.
which implies the claim.
Tex syntax errorfirst. It is a standard fact that this ring is isomorphic to
Tex syntax error
where the last equality holds since we are in characteristic  .
.
Tex syntax erroris local. This can be shown as follows. Suppose
Tex syntax erroris a maximal ideal. We let
Tex syntax errorbe its preimage under the canonical projection. It is a prime ideal that contains the ideal
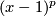 and hence must contain the ideal
and hence must contain the ideal  . But since
. But since  is maximal in
is maximal in Tex syntax errorwe must have equality, i.e.,
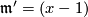 and hence
and hence  is the image of the ideal generated by
is the image of the ideal generated by  which determines
which determines  uniquely. Thus
uniquely. Thus Tex syntax errorhas a unique maximal ideal. So we have shown that
Tex syntax erroris a local ring. In particular every element fulfills that either
 or
or 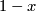 is invertible (in a local ring the complement of the maximal ideal consists of the units). Thus if
is invertible (in a local ring the complement of the maximal ideal consists of the units). Thus if  is an idempotent it must be
is an idempotent it must be  or
or  .
We can put this in more geometric terms as follows. The ring
.
We can put this in more geometric terms as follows. The ring Tex syntax erroris a local, artinian ring (this ring is not only finitely generated as an
Tex syntax error-algebra but also as an
Tex syntax error-module and is thus artinian) and hence its spectrum consists of precisely one point (every prime ideal is maximal). But a non-trivial idempotent
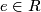 for any ring decomposes the ring into the product
for any ring decomposes the ring into the product 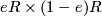 and hence the spectrum of
and hence the spectrum of  is a disjoint union of two non-empty subsets. Of course, this cannot be the case if the spectrum consists only of one point.
is a disjoint union of two non-empty subsets. Of course, this cannot be the case if the spectrum consists only of one point.
We now claim that also in the ring 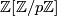 for general prime numbers
for general prime numbers  there are only the trivial idempotents. This follows from the previous considerations as follows.
there are only the trivial idempotents. This follows from the previous considerations as follows.
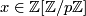 . Then we have just shown that the reduction mod
. Then we have just shown that the reduction mod  of
of  is either
is either  or
or  . Without loss of generality we may assume that it is zero. But then it follows that
. Without loss of generality we may assume that it is zero. But then it follows that 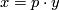 for some
for some 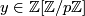 . But since
. But since  is an idempotent it fulfills
is an idempotent it fulfills 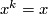 for all
for all  . Calculating
. Calculating 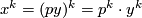 shows that
shows that  is divisible by
is divisible by 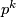 for all
for all  which implies that
which implies that Tex syntax error. $-dimensional as the group is abelian. Hence the idempotents of
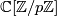 are precisely
are precisely  -tupels with entries either
-tupels with entries either  or
or  , since
, since 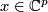 fulfills
fulfills 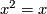 if and only if each
if and only if each 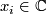 fulfills
fulfills 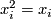 which implies the claim.
Let us turn to the other two rings and let us focus on the case
which implies the claim.
Let us turn to the other two rings and let us focus on the case Tex syntax errorfirst. It is a standard fact that this ring is isomorphic to
Tex syntax error
where the last equality holds since we are in characteristic  .
.
Tex syntax erroris local. This can be shown as follows. Suppose
Tex syntax erroris a maximal ideal. We let
Tex syntax errorbe its preimage under the canonical projection. It is a prime ideal that contains the ideal
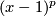 and hence must contain the ideal
and hence must contain the ideal  . But since
. But since  is maximal in
is maximal in Tex syntax errorwe must have equality, i.e.,
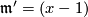 and hence
and hence  is the image of the ideal generated by
is the image of the ideal generated by  which determines
which determines  uniquely. Thus
uniquely. Thus Tex syntax errorhas a unique maximal ideal. So we have shown that
Tex syntax erroris a local ring. In particular every element fulfills that either
 or
or 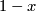 is invertible (in a local ring the complement of the maximal ideal consists of the units). Thus if
is invertible (in a local ring the complement of the maximal ideal consists of the units). Thus if  is an idempotent it must be
is an idempotent it must be  or
or  .
We can put this in more geometric terms as follows. The ring
.
We can put this in more geometric terms as follows. The ring Tex syntax erroris a local, artinian ring (this ring is not only finitely generated as an
Tex syntax error-algebra but also as an
Tex syntax error-module and is thus artinian) and hence its spectrum consists of precisely one point (every prime ideal is maximal). But a non-trivial idempotent
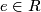 for any ring decomposes the ring into the product
for any ring decomposes the ring into the product 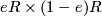 and hence the spectrum of
and hence the spectrum of  is a disjoint union of two non-empty subsets. Of course, this cannot be the case if the spectrum consists only of one point.
is a disjoint union of two non-empty subsets. Of course, this cannot be the case if the spectrum consists only of one point.
We now claim that also in the ring 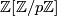 for general prime numbers
for general prime numbers  there are only the trivial idempotents. This follows from the previous considerations as follows.
there are only the trivial idempotents. This follows from the previous considerations as follows.
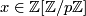 . Then we have just shown that the reduction mod
. Then we have just shown that the reduction mod  of
of  is either
is either  or
or  . Without loss of generality we may assume that it is zero. But then it follows that
. Without loss of generality we may assume that it is zero. But then it follows that 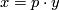 for some
for some 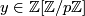 . But since
. But since  is an idempotent it fulfills
is an idempotent it fulfills 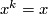 for all
for all  . Calculating
. Calculating 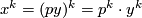 shows that
shows that  is divisible by
is divisible by 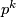 for all
for all  which implies that
which implies that Tex syntax error. $
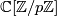 are precisely
are precisely  -tupels with entries either
-tupels with entries either  or
or  , since
, since 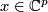 fulfills
fulfills 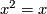 if and only if each
if and only if each 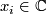 fulfills
fulfills 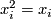 which implies the claim.
Let us turn to the other two rings and let us focus on the case
which implies the claim.
Let us turn to the other two rings and let us focus on the case Tex syntax errorfirst. It is a standard fact that this ring is isomorphic to
Tex syntax error
where the last equality holds since we are in characteristic  .
.
Tex syntax erroris local. This can be shown as follows. Suppose
Tex syntax erroris a maximal ideal. We let
Tex syntax errorbe its preimage under the canonical projection. It is a prime ideal that contains the ideal
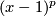 and hence must contain the ideal
and hence must contain the ideal  . But since
. But since  is maximal in
is maximal in Tex syntax errorwe must have equality, i.e.,
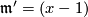 and hence
and hence  is the image of the ideal generated by
is the image of the ideal generated by  which determines
which determines  uniquely. Thus
uniquely. Thus Tex syntax errorhas a unique maximal ideal. So we have shown that
Tex syntax erroris a local ring. In particular every element fulfills that either
 or
or 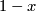 is invertible (in a local ring the complement of the maximal ideal consists of the units). Thus if
is invertible (in a local ring the complement of the maximal ideal consists of the units). Thus if  is an idempotent it must be
is an idempotent it must be  or
or  .
We can put this in more geometric terms as follows. The ring
.
We can put this in more geometric terms as follows. The ring Tex syntax erroris a local, artinian ring (this ring is not only finitely generated as an
Tex syntax error-algebra but also as an
Tex syntax error-module and is thus artinian) and hence its spectrum consists of precisely one point (every prime ideal is maximal). But a non-trivial idempotent
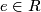 for any ring decomposes the ring into the product
for any ring decomposes the ring into the product 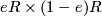 and hence the spectrum of
and hence the spectrum of  is a disjoint union of two non-empty subsets. Of course, this cannot be the case if the spectrum consists only of one point.
is a disjoint union of two non-empty subsets. Of course, this cannot be the case if the spectrum consists only of one point.
We now claim that also in the ring 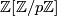 for general prime numbers
for general prime numbers  there are only the trivial idempotents. This follows from the previous considerations as follows.
there are only the trivial idempotents. This follows from the previous considerations as follows.
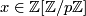 . Then we have just shown that the reduction mod
. Then we have just shown that the reduction mod  of
of  is either
is either  or
or  . Without loss of generality we may assume that it is zero. But then it follows that
. Without loss of generality we may assume that it is zero. But then it follows that 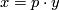 for some
for some 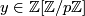 . But since
. But since  is an idempotent it fulfills
is an idempotent it fulfills 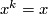 for all
for all  . Calculating
. Calculating 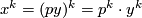 shows that
shows that  is divisible by
is divisible by 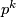 for all
for all  which implies that
which implies that Tex syntax error. $
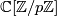 are precisely
are precisely  -tupels with entries either
-tupels with entries either  or
or  , since
, since 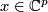 fulfills
fulfills 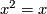 if and only if each
if and only if each 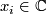 fulfills
fulfills 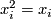 which implies the claim.
Let us turn to the other two rings and let us focus on the case
which implies the claim.
Let us turn to the other two rings and let us focus on the case Tex syntax errorfirst. It is a standard fact that this ring is isomorphic to
Tex syntax error
where the last equality holds since we are in characteristic  .
.
Tex syntax erroris local. This can be shown as follows. Suppose
Tex syntax erroris a maximal ideal. We let
Tex syntax errorbe its preimage under the canonical projection. It is a prime ideal that contains the ideal
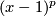 and hence must contain the ideal
and hence must contain the ideal  . But since
. But since  is maximal in
is maximal in Tex syntax errorwe must have equality, i.e.,
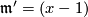 and hence
and hence  is the image of the ideal generated by
is the image of the ideal generated by  which determines
which determines  uniquely. Thus
uniquely. Thus Tex syntax errorhas a unique maximal ideal. So we have shown that
Tex syntax erroris a local ring. In particular every element fulfills that either
 or
or 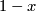 is invertible (in a local ring the complement of the maximal ideal consists of the units). Thus if
is invertible (in a local ring the complement of the maximal ideal consists of the units). Thus if  is an idempotent it must be
is an idempotent it must be  or
or  .
We can put this in more geometric terms as follows. The ring
.
We can put this in more geometric terms as follows. The ring Tex syntax erroris a local, artinian ring (this ring is not only finitely generated as an
Tex syntax error-algebra but also as an
Tex syntax error-module and is thus artinian) and hence its spectrum consists of precisely one point (every prime ideal is maximal). But a non-trivial idempotent
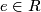 for any ring decomposes the ring into the product
for any ring decomposes the ring into the product 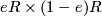 and hence the spectrum of
and hence the spectrum of  is a disjoint union of two non-empty subsets. Of course, this cannot be the case if the spectrum consists only of one point.
is a disjoint union of two non-empty subsets. Of course, this cannot be the case if the spectrum consists only of one point.
We now claim that also in the ring 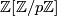 for general prime numbers
for general prime numbers  there are only the trivial idempotents. This follows from the previous considerations as follows.
there are only the trivial idempotents. This follows from the previous considerations as follows.
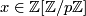 . Then we have just shown that the reduction mod
. Then we have just shown that the reduction mod  of
of  is either
is either  or
or  . Without loss of generality we may assume that it is zero. But then it follows that
. Without loss of generality we may assume that it is zero. But then it follows that 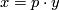 for some
for some 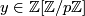 . But since
. But since  is an idempotent it fulfills
is an idempotent it fulfills 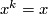 for all
for all  . Calculating
. Calculating 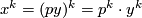 shows that
shows that  is divisible by
is divisible by 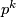 for all
for all  which implies that
which implies that Tex syntax error. -x$
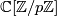 are precisely
are precisely  -tupels with entries either
-tupels with entries either  or
or  , since
, since 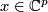 fulfills
fulfills 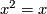 if and only if each
if and only if each 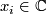 fulfills
fulfills 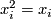 which implies the claim.
Let us turn to the other two rings and let us focus on the case
which implies the claim.
Let us turn to the other two rings and let us focus on the case Tex syntax errorfirst. It is a standard fact that this ring is isomorphic to
Tex syntax error
where the last equality holds since we are in characteristic  .
.
Tex syntax erroris local. This can be shown as follows. Suppose
Tex syntax erroris a maximal ideal. We let
Tex syntax errorbe its preimage under the canonical projection. It is a prime ideal that contains the ideal
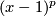 and hence must contain the ideal
and hence must contain the ideal  . But since
. But since  is maximal in
is maximal in Tex syntax errorwe must have equality, i.e.,
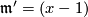 and hence
and hence  is the image of the ideal generated by
is the image of the ideal generated by  which determines
which determines  uniquely. Thus
uniquely. Thus Tex syntax errorhas a unique maximal ideal. So we have shown that
Tex syntax erroris a local ring. In particular every element fulfills that either
 or
or 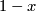 is invertible (in a local ring the complement of the maximal ideal consists of the units). Thus if
is invertible (in a local ring the complement of the maximal ideal consists of the units). Thus if  is an idempotent it must be
is an idempotent it must be  or
or  .
We can put this in more geometric terms as follows. The ring
.
We can put this in more geometric terms as follows. The ring Tex syntax erroris a local, artinian ring (this ring is not only finitely generated as an
Tex syntax error-algebra but also as an
Tex syntax error-module and is thus artinian) and hence its spectrum consists of precisely one point (every prime ideal is maximal). But a non-trivial idempotent
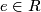 for any ring decomposes the ring into the product
for any ring decomposes the ring into the product 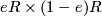 and hence the spectrum of
and hence the spectrum of  is a disjoint union of two non-empty subsets. Of course, this cannot be the case if the spectrum consists only of one point.
is a disjoint union of two non-empty subsets. Of course, this cannot be the case if the spectrum consists only of one point.
We now claim that also in the ring 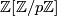 for general prime numbers
for general prime numbers  there are only the trivial idempotents. This follows from the previous considerations as follows.
there are only the trivial idempotents. This follows from the previous considerations as follows.
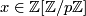 . Then we have just shown that the reduction mod
. Then we have just shown that the reduction mod  of
of  is either
is either  or
or  . Without loss of generality we may assume that it is zero. But then it follows that
. Without loss of generality we may assume that it is zero. But then it follows that 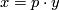 for some
for some 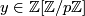 . But since
. But since  is an idempotent it fulfills
is an idempotent it fulfills 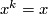 for all
for all  . Calculating
. Calculating 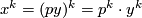 shows that
shows that  is divisible by
is divisible by 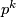 for all
for all  which implies that
which implies that Tex syntax error. $
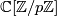 are precisely
are precisely  -tupels with entries either
-tupels with entries either  or
or  , since
, since 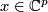 fulfills
fulfills 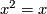 if and only if each
if and only if each 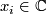 fulfills
fulfills 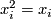 which implies the claim.
Let us turn to the other two rings and let us focus on the case
which implies the claim.
Let us turn to the other two rings and let us focus on the case Tex syntax errorfirst. It is a standard fact that this ring is isomorphic to
Tex syntax error
where the last equality holds since we are in characteristic  .
.
Tex syntax erroris local. This can be shown as follows. Suppose
Tex syntax erroris a maximal ideal. We let
Tex syntax errorbe its preimage under the canonical projection. It is a prime ideal that contains the ideal
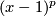 and hence must contain the ideal
and hence must contain the ideal  . But since
. But since  is maximal in
is maximal in Tex syntax errorwe must have equality, i.e.,
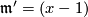 and hence
and hence  is the image of the ideal generated by
is the image of the ideal generated by  which determines
which determines  uniquely. Thus
uniquely. Thus Tex syntax errorhas a unique maximal ideal. So we have shown that
Tex syntax erroris a local ring. In particular every element fulfills that either
 or
or 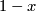 is invertible (in a local ring the complement of the maximal ideal consists of the units). Thus if
is invertible (in a local ring the complement of the maximal ideal consists of the units). Thus if  is an idempotent it must be
is an idempotent it must be  or
or  .
We can put this in more geometric terms as follows. The ring
.
We can put this in more geometric terms as follows. The ring Tex syntax erroris a local, artinian ring (this ring is not only finitely generated as an
Tex syntax error-algebra but also as an
Tex syntax error-module and is thus artinian) and hence its spectrum consists of precisely one point (every prime ideal is maximal). But a non-trivial idempotent
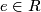 for any ring decomposes the ring into the product
for any ring decomposes the ring into the product 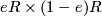 and hence the spectrum of
and hence the spectrum of  is a disjoint union of two non-empty subsets. Of course, this cannot be the case if the spectrum consists only of one point.
is a disjoint union of two non-empty subsets. Of course, this cannot be the case if the spectrum consists only of one point.
We now claim that also in the ring 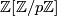 for general prime numbers
for general prime numbers  there are only the trivial idempotents. This follows from the previous considerations as follows.
there are only the trivial idempotents. This follows from the previous considerations as follows.
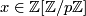 . Then we have just shown that the reduction mod
. Then we have just shown that the reduction mod  of
of  is either
is either  or
or  . Without loss of generality we may assume that it is zero. But then it follows that
. Without loss of generality we may assume that it is zero. But then it follows that 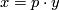 for some
for some 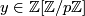 . But since
. But since  is an idempotent it fulfills
is an idempotent it fulfills 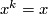 for all
for all  . Calculating
. Calculating 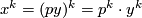 shows that
shows that  is divisible by
is divisible by 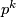 for all
for all  which implies that
which implies that Tex syntax error. $
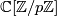 are precisely
are precisely  -tupels with entries either
-tupels with entries either  or
or  , since
, since 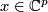 fulfills
fulfills 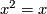 if and only if each
if and only if each 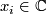 fulfills
fulfills 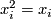 which implies the claim.
Let us turn to the other two rings and let us focus on the case
which implies the claim.
Let us turn to the other two rings and let us focus on the case Tex syntax errorfirst. It is a standard fact that this ring is isomorphic to
Tex syntax error
where the last equality holds since we are in characteristic  .
.
Tex syntax erroris local. This can be shown as follows. Suppose
Tex syntax erroris a maximal ideal. We let
Tex syntax errorbe its preimage under the canonical projection. It is a prime ideal that contains the ideal
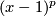 and hence must contain the ideal
and hence must contain the ideal  . But since
. But since  is maximal in
is maximal in Tex syntax errorwe must have equality, i.e.,
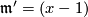 and hence
and hence  is the image of the ideal generated by
is the image of the ideal generated by  which determines
which determines  uniquely. Thus
uniquely. Thus Tex syntax errorhas a unique maximal ideal. So we have shown that
Tex syntax erroris a local ring. In particular every element fulfills that either
 or
or 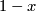 is invertible (in a local ring the complement of the maximal ideal consists of the units). Thus if
is invertible (in a local ring the complement of the maximal ideal consists of the units). Thus if  is an idempotent it must be
is an idempotent it must be  or
or  .
We can put this in more geometric terms as follows. The ring
.
We can put this in more geometric terms as follows. The ring Tex syntax erroris a local, artinian ring (this ring is not only finitely generated as an
Tex syntax error-algebra but also as an
Tex syntax error-module and is thus artinian) and hence its spectrum consists of precisely one point (every prime ideal is maximal). But a non-trivial idempotent
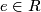 for any ring decomposes the ring into the product
for any ring decomposes the ring into the product 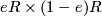 and hence the spectrum of
and hence the spectrum of  is a disjoint union of two non-empty subsets. Of course, this cannot be the case if the spectrum consists only of one point.
is a disjoint union of two non-empty subsets. Of course, this cannot be the case if the spectrum consists only of one point.
We now claim that also in the ring 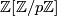 for general prime numbers
for general prime numbers  there are only the trivial idempotents. This follows from the previous considerations as follows.
there are only the trivial idempotents. This follows from the previous considerations as follows.
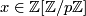 . Then we have just shown that the reduction mod
. Then we have just shown that the reduction mod  of
of  is either
is either  or
or  . Without loss of generality we may assume that it is zero. But then it follows that
. Without loss of generality we may assume that it is zero. But then it follows that 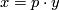 for some
for some 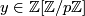 . But since
. But since  is an idempotent it fulfills
is an idempotent it fulfills 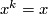 for all
for all  . Calculating
. Calculating 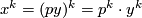 shows that
shows that  is divisible by
is divisible by 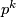 for all
for all  which implies that
which implies that Tex syntax error. $
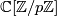 are precisely
are precisely  -tupels with entries either
-tupels with entries either  or
or  , since
, since 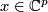 fulfills
fulfills 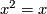 if and only if each
if and only if each 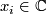 fulfills
fulfills 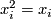 which implies the claim.
Let us turn to the other two rings and let us focus on the case
which implies the claim.
Let us turn to the other two rings and let us focus on the case Tex syntax errorfirst. It is a standard fact that this ring is isomorphic to
Tex syntax error
where the last equality holds since we are in characteristic  .
.
Tex syntax erroris local. This can be shown as follows. Suppose
Tex syntax erroris a maximal ideal. We let
Tex syntax errorbe its preimage under the canonical projection. It is a prime ideal that contains the ideal
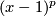 and hence must contain the ideal
and hence must contain the ideal  . But since
. But since  is maximal in
is maximal in Tex syntax errorwe must have equality, i.e.,
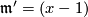 and hence
and hence  is the image of the ideal generated by
is the image of the ideal generated by  which determines
which determines  uniquely. Thus
uniquely. Thus Tex syntax errorhas a unique maximal ideal. So we have shown that
Tex syntax erroris a local ring. In particular every element fulfills that either
 or
or 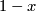 is invertible (in a local ring the complement of the maximal ideal consists of the units). Thus if
is invertible (in a local ring the complement of the maximal ideal consists of the units). Thus if  is an idempotent it must be
is an idempotent it must be  or
or  .
We can put this in more geometric terms as follows. The ring
.
We can put this in more geometric terms as follows. The ring Tex syntax erroris a local, artinian ring (this ring is not only finitely generated as an
Tex syntax error-algebra but also as an
Tex syntax error-module and is thus artinian) and hence its spectrum consists of precisely one point (every prime ideal is maximal). But a non-trivial idempotent
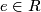 for any ring decomposes the ring into the product
for any ring decomposes the ring into the product 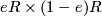 and hence the spectrum of
and hence the spectrum of  is a disjoint union of two non-empty subsets. Of course, this cannot be the case if the spectrum consists only of one point.
is a disjoint union of two non-empty subsets. Of course, this cannot be the case if the spectrum consists only of one point.
We now claim that also in the ring 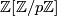 for general prime numbers
for general prime numbers  there are only the trivial idempotents. This follows from the previous considerations as follows.
there are only the trivial idempotents. This follows from the previous considerations as follows.
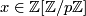 . Then we have just shown that the reduction mod
. Then we have just shown that the reduction mod  of
of  is either
is either  or
or  . Without loss of generality we may assume that it is zero. But then it follows that
. Without loss of generality we may assume that it is zero. But then it follows that 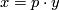 for some
for some 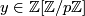 . But since
. But since  is an idempotent it fulfills
is an idempotent it fulfills 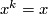 for all
for all  . Calculating
. Calculating 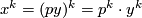 shows that
shows that  is divisible by
is divisible by 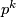 for all
for all  which implies that
which implies that Tex syntax error. $
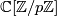 are precisely
are precisely  -tupels with entries either
-tupels with entries either  or
or  , since
, since 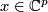 fulfills
fulfills 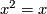 if and only if each
if and only if each 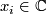 fulfills
fulfills 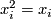 which implies the claim.
Let us turn to the other two rings and let us focus on the case
which implies the claim.
Let us turn to the other two rings and let us focus on the case Tex syntax errorfirst. It is a standard fact that this ring is isomorphic to
Tex syntax error
where the last equality holds since we are in characteristic  .
.
Tex syntax erroris local. This can be shown as follows. Suppose
Tex syntax erroris a maximal ideal. We let
Tex syntax errorbe its preimage under the canonical projection. It is a prime ideal that contains the ideal
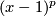 and hence must contain the ideal
and hence must contain the ideal  . But since
. But since  is maximal in
is maximal in Tex syntax errorwe must have equality, i.e.,
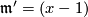 and hence
and hence  is the image of the ideal generated by
is the image of the ideal generated by  which determines
which determines  uniquely. Thus
uniquely. Thus Tex syntax errorhas a unique maximal ideal. So we have shown that
Tex syntax erroris a local ring. In particular every element fulfills that either
 or
or 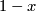 is invertible (in a local ring the complement of the maximal ideal consists of the units). Thus if
is invertible (in a local ring the complement of the maximal ideal consists of the units). Thus if  is an idempotent it must be
is an idempotent it must be  or
or  .
We can put this in more geometric terms as follows. The ring
.
We can put this in more geometric terms as follows. The ring Tex syntax erroris a local, artinian ring (this ring is not only finitely generated as an
Tex syntax error-algebra but also as an
Tex syntax error-module and is thus artinian) and hence its spectrum consists of precisely one point (every prime ideal is maximal). But a non-trivial idempotent
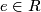 for any ring decomposes the ring into the product
for any ring decomposes the ring into the product 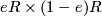 and hence the spectrum of
and hence the spectrum of  is a disjoint union of two non-empty subsets. Of course, this cannot be the case if the spectrum consists only of one point.
is a disjoint union of two non-empty subsets. Of course, this cannot be the case if the spectrum consists only of one point.
We now claim that also in the ring 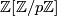 for general prime numbers
for general prime numbers  there are only the trivial idempotents. This follows from the previous considerations as follows.
there are only the trivial idempotents. This follows from the previous considerations as follows.
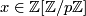 . Then we have just shown that the reduction mod
. Then we have just shown that the reduction mod  of
of  is either
is either  or
or  . Without loss of generality we may assume that it is zero. But then it follows that
. Without loss of generality we may assume that it is zero. But then it follows that 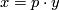 for some
for some 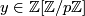 . But since
. But since  is an idempotent it fulfills
is an idempotent it fulfills 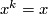 for all
for all  . Calculating
. Calculating 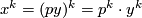 shows that
shows that  is divisible by
is divisible by 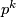 for all
for all  which implies that
which implies that Tex syntax error.