Talk:Equivariant homology (Ex)
Markus Land (Talk | contribs) (Created page with "<wikitex>; We can simply use the Borel-construction for equivariant homology. This takes an unequivariant homology theory $\mathcal{K}$ and defines for a group $G$ and any $G...") |
Markus Land (Talk | contribs) |
||
| Line 8: | Line 8: | ||
as $EG$ is a contractible space on which $H \subset G$ acts freely, and hence $EG$ is a model for $EH$. | as $EG$ is a contractible space on which $H \subset G$ acts freely, and hence $EG$ is a model for $EH$. | ||
| + | This also comes from a functor from groupoids to spectra as follows: | ||
| + | |||
| + | Given a groupoid $\mathcal{G}$ we associate to it the spectrum | ||
| + | $$ | \mathcal{N}( \mathcal{G}) | _{+} \wedge \mathcal{K}$$ | ||
| + | where we view $\mathcal{K}$ as the spectrum associated to the unequivariant homology theory $\mathcal{K}$. | ||
| + | |||
| + | To see what the $G$-homology theory $\mathcal{K}^G$ is, it suffices to understand the composite functor | ||
| + | $$\xymatrix{ Or(G) \ar[r] & \text{groupoids} \ar[r] & \text{Sp} } $$ | ||
| + | where the functor $Or(G) \to \text{groupoids}$ takes a homogenous space $G/H$ to its transport groupoid $\overline{G/H}$, which is equivalent to the group $H$ viewed as groupoid. | ||
| + | |||
| + | Hence we see that $$| \mathcal{N}(\overline{G/H})|_+ \wedge \mathcal{K} \simeq |\mathcal{N}(H)|_+ \mathcal{K} \simeq BH_+\wedge \mathcal{K}.$$ | ||
| + | |||
| + | Thus we see that we have the correct coefficients as stated in the exercise and a little computation in coends also shows that the equivariant homology theory associated to this groupoid-spectrum is given by the above Borel-construction. | ||
</wikitex> | </wikitex> | ||
Latest revision as of 13:19, 2 September 2013
We can simply use the Borel-construction for equivariant homology. This takes an unequivariant homology theory 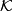 and defines for a group
and defines for a group  and any
and any  -space
-space  the
the  -equivariant homology to be
-equivariant homology to be
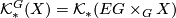
i.e., the equivariant homology of  is the unequivariant homology of the homotopy orbits of the
is the unequivariant homology of the homotopy orbits of the  -action on
-action on  .
Of course we then get
.
Of course we then get
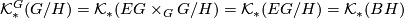
as 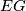 is a contractible space on which
is a contractible space on which  acts freely, and hence
acts freely, and hence 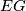 is a model for
is a model for 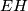 .
.
This also comes from a functor from groupoids to spectra as follows:
Given a groupoid 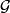 we associate to it the spectrum
we associate to it the spectrum
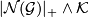
where we view 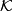 as the spectrum associated to the unequivariant homology theory
as the spectrum associated to the unequivariant homology theory 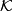 .
.
To see what the  -homology theory
-homology theory 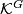 is, it suffices to understand the composite functor
is, it suffices to understand the composite functor
![\displaystyle \xymatrix{ Or(G) \ar[r] & \text{groupoids} \ar[r] & \text{Sp} }](/images/math/f/9/3/f93856e656e3eb1ca4af2ec77d229c4c.png)
where the functor 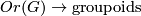 takes a homogenous space
takes a homogenous space 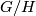 to its transport groupoid
to its transport groupoid 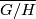 , which is equivalent to the group
, which is equivalent to the group  viewed as groupoid.
viewed as groupoid.
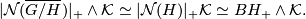
Thus we see that we have the correct coefficients as stated in the exercise and a little computation in coends also shows that the equivariant homology theory associated to this groupoid-spectrum is given by the above Borel-construction.