Talk:Elementary invariants of Heegaard diagrams (Ex)
The Heegaard diagram 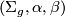 naturally gives a handle structure on
naturally gives a handle structure on  . The handlebody
. The handlebody 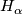 consists of the
consists of the  -handle and
-handle and 
 -handles, whose belt spheres are the
-handles, whose belt spheres are the  curves. The handlebody
curves. The handlebody 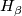 consists of the
consists of the  -handle and
-handle and 
 -handles (this is a relative handle decomposition of
-handles (this is a relative handle decomposition of 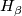 ). The attaching spheres of the
). The attaching spheres of the  -handles are the
-handles are the  curves.
curves.
We will give group presentations for 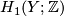 and
and 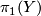 with generators corresponding to the
with generators corresponding to the  curves (which are in correspondence with the
curves (which are in correspondence with the  -handles). We obtain a relation for each
-handles). We obtain a relation for each  -handle (which are in correspondence with the
-handle (which are in correspondence with the  curves). The
curves). The  curves describe the attaching maps of the
curves describe the attaching maps of the  -handles; thus we can compute
-handles; thus we can compute 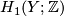 and
and 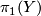 by investigating the intersections of the
by investigating the intersections of the  and
and  curves, as each intersection marks a
curves, as each intersection marks a  -handle attaching circle traveling geometrically once over a
-handle attaching circle traveling geometrically once over a  -handle.
-handle.
Let ![\gamma_{ij}=\gamma([\alpha_i],[\beta_j])](/images/math/1/e/9/1e9be0fff620893746fb6d430d6953c4.png) indicate the algebraic intersection of
indicate the algebraic intersection of 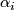 with
with 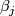 . Then
. Then ![H_1(Y;\mathbb{Z})\cong\langle x_1,\ldots, x_g\mid [x_i,x_j]\forall(i,j), \sum_{i=1}^g\gamma_{ij}x_i\forall j\rangle](/images/math/6/5/c/65c9d2bfb6315c384516c221c0bf0a2e.png) .
.
Now pick a basepoint 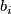 for each
for each 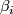 . Traveling once around
. Traveling once around 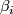 starting at
starting at 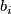 , say that
, say that 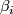 intersects
intersects 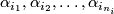 in order (with each entry indicating one intersection), with sign
in order (with each entry indicating one intersection), with sign 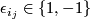 . Let
. Let 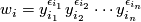 . Then
. Then 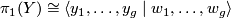 .
.
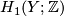 and
and 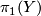 with group presentations, we can write the Hurewicz map
with group presentations, we can write the Hurewicz map 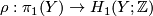 as the map
as the map ![\displaystyle \rho:\left\langle x_1,\ldots, x_g\mid [x_i,x_j]\forall(i,j), \sum_{i=1}^g\gamma_{ij}x_i\forall j\right\rangle\to\langle y_1,\ldots, y_g\mid w_1,\ldots, w_g\rangle](/images/math/a/f/3/af39ce0ad287fc00f87e0a5355cb6cb5.png)
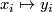 For each
For each 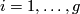 .
.
 . The handlebody
. The handlebody 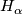 consists of the
consists of the  -handle and
-handle and 
 -handles, whose belt spheres are the
-handles, whose belt spheres are the  curves. The handlebody
curves. The handlebody 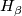 consists of the
consists of the  -handle and
-handle and 
 -handles (this is a relative handle decomposition of
-handles (this is a relative handle decomposition of 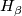 ). The attaching spheres of the
). The attaching spheres of the  -handles are the
-handles are the  curves.
curves.
We will give group presentations for 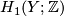 and
and 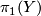 with generators corresponding to the
with generators corresponding to the  curves (which are in correspondence with the
curves (which are in correspondence with the  -handles). We obtain a relation for each
-handles). We obtain a relation for each  -handle (which are in correspondence with the
-handle (which are in correspondence with the  curves). The
curves). The  curves describe the attaching maps of the
curves describe the attaching maps of the  -handles; thus we can compute
-handles; thus we can compute 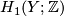 and
and 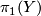 by investigating the intersections of the
by investigating the intersections of the  and
and  curves, as each intersection marks a
curves, as each intersection marks a  -handle attaching circle traveling geometrically once over a
-handle attaching circle traveling geometrically once over a  -handle.
-handle.
Let ![\gamma_{ij}=\gamma([\alpha_i],[\beta_j])](/images/math/1/e/9/1e9be0fff620893746fb6d430d6953c4.png) indicate the algebraic intersection of
indicate the algebraic intersection of 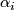 with
with 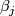 . Then
. Then ![H_1(Y;\mathbb{Z})\cong\langle x_1,\ldots, x_g\mid [x_i,x_j]\forall(i,j), \sum_{i=1}^g\gamma_{ij}x_i\forall j\rangle](/images/math/6/5/c/65c9d2bfb6315c384516c221c0bf0a2e.png) .
.
Now pick a basepoint 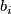 for each
for each 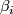 . Traveling once around
. Traveling once around 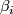 starting at
starting at 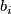 , say that
, say that 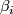 intersects
intersects 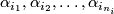 in order (with each entry indicating one intersection), with sign
in order (with each entry indicating one intersection), with sign 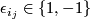 . Let
. Let 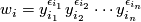 . Then
. Then 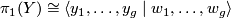 .
.
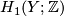 and
and 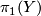 with group presentations, we can write the Hurewicz map
with group presentations, we can write the Hurewicz map 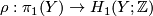 as the map
as the map ![\displaystyle \rho:\left\langle x_1,\ldots, x_g\mid [x_i,x_j]\forall(i,j), \sum_{i=1}^g\gamma_{ij}x_i\forall j\right\rangle\to\langle y_1,\ldots, y_g\mid w_1,\ldots, w_g\rangle](/images/math/a/f/3/af39ce0ad287fc00f87e0a5355cb6cb5.png)
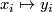 For each
For each 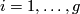 .
.
 . The handlebody
. The handlebody 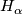 consists of the
consists of the  -handle and
-handle and 
 -handles, whose belt spheres are the
-handles, whose belt spheres are the  curves. The handlebody
curves. The handlebody 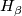 consists of the
consists of the  -handle and
-handle and 
 -handles (this is a relative handle decomposition of
-handles (this is a relative handle decomposition of 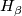 ). The attaching spheres of the
). The attaching spheres of the  -handles are the
-handles are the  curves.
curves.
We will give group presentations for 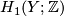 and
and 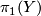 with generators corresponding to the
with generators corresponding to the  curves (which are in correspondence with the
curves (which are in correspondence with the  -handles). We obtain a relation for each
-handles). We obtain a relation for each  -handle (which are in correspondence with the
-handle (which are in correspondence with the  curves). The
curves). The  curves describe the attaching maps of the
curves describe the attaching maps of the  -handles; thus we can compute
-handles; thus we can compute 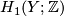 and
and 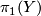 by investigating the intersections of the
by investigating the intersections of the  and
and  curves, as each intersection marks a
curves, as each intersection marks a  -handle attaching circle traveling geometrically once over a
-handle attaching circle traveling geometrically once over a  -handle.
-handle.
Let ![\gamma_{ij}=\gamma([\alpha_i],[\beta_j])](/images/math/1/e/9/1e9be0fff620893746fb6d430d6953c4.png) indicate the algebraic intersection of
indicate the algebraic intersection of 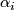 with
with 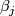 . Then
. Then ![H_1(Y;\mathbb{Z})\cong\langle x_1,\ldots, x_g\mid [x_i,x_j]\forall(i,j), \sum_{i=1}^g\gamma_{ij}x_i\forall j\rangle](/images/math/6/5/c/65c9d2bfb6315c384516c221c0bf0a2e.png) .
.
Now pick a basepoint 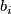 for each
for each 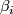 . Traveling once around
. Traveling once around 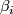 starting at
starting at 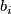 , say that
, say that 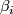 intersects
intersects 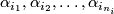 in order (with each entry indicating one intersection), with sign
in order (with each entry indicating one intersection), with sign 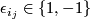 . Let
. Let 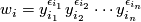 . Then
. Then 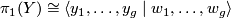 .
.
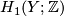 and
and 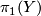 with group presentations, we can write the Hurewicz map
with group presentations, we can write the Hurewicz map 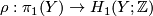 as the map
as the map ![\displaystyle \rho:\left\langle x_1,\ldots, x_g\mid [x_i,x_j]\forall(i,j), \sum_{i=1}^g\gamma_{ij}x_i\forall j\right\rangle\to\langle y_1,\ldots, y_g\mid w_1,\ldots, w_g\rangle](/images/math/a/f/3/af39ce0ad287fc00f87e0a5355cb6cb5.png)
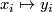 For each
For each 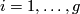 .
.
 . The handlebody
. The handlebody 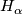 consists of the
consists of the  -handle and
-handle and 
 -handles, whose belt spheres are the
-handles, whose belt spheres are the  curves. The handlebody
curves. The handlebody 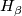 consists of the
consists of the  -handle and
-handle and 
 -handles (this is a relative handle decomposition of
-handles (this is a relative handle decomposition of 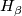 ). The attaching spheres of the
). The attaching spheres of the  -handles are the
-handles are the  curves.
curves.
We will give group presentations for 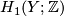 and
and 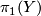 with generators corresponding to the
with generators corresponding to the  curves (which are in correspondence with the
curves (which are in correspondence with the  -handles). We obtain a relation for each
-handles). We obtain a relation for each  -handle (which are in correspondence with the
-handle (which are in correspondence with the  curves). The
curves). The  curves describe the attaching maps of the
curves describe the attaching maps of the  -handles; thus we can compute
-handles; thus we can compute 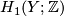 and
and 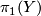 by investigating the intersections of the
by investigating the intersections of the  and
and  curves, as each intersection marks a
curves, as each intersection marks a  -handle attaching circle traveling geometrically once over a
-handle attaching circle traveling geometrically once over a  -handle.
-handle.
Let ![\gamma_{ij}=\gamma([\alpha_i],[\beta_j])](/images/math/1/e/9/1e9be0fff620893746fb6d430d6953c4.png) indicate the algebraic intersection of
indicate the algebraic intersection of 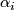 with
with 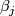 . Then
. Then ![H_1(Y;\mathbb{Z})\cong\langle x_1,\ldots, x_g\mid [x_i,x_j]\forall(i,j), \sum_{i=1}^g\gamma_{ij}x_i\forall j\rangle](/images/math/6/5/c/65c9d2bfb6315c384516c221c0bf0a2e.png) .
.
Now pick a basepoint 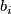 for each
for each 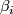 . Traveling once around
. Traveling once around 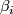 starting at
starting at 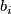 , say that
, say that 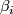 intersects
intersects 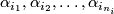 in order (with each entry indicating one intersection), with sign
in order (with each entry indicating one intersection), with sign 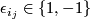 . Let
. Let 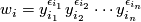 . Then
. Then 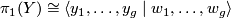 .
.
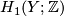 and
and 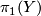 with group presentations, we can write the Hurewicz map
with group presentations, we can write the Hurewicz map 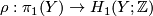 as the map
as the map ![\displaystyle \rho:\left\langle x_1,\ldots, x_g\mid [x_i,x_j]\forall(i,j), \sum_{i=1}^g\gamma_{ij}x_i\forall j\right\rangle\to\langle y_1,\ldots, y_g\mid w_1,\ldots, w_g\rangle](/images/math/a/f/3/af39ce0ad287fc00f87e0a5355cb6cb5.png)
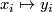 For each
For each 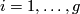 .
.
 . The handlebody
. The handlebody 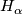 consists of the
consists of the  -handle and
-handle and 
 -handles, whose belt spheres are the
-handles, whose belt spheres are the  curves. The handlebody
curves. The handlebody 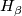 consists of the
consists of the  -handle and
-handle and 
 -handles (this is a relative handle decomposition of
-handles (this is a relative handle decomposition of 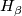 ). The attaching spheres of the
). The attaching spheres of the  -handles are the
-handles are the  curves.
curves.
We will give group presentations for 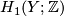 and
and 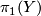 with generators corresponding to the
with generators corresponding to the  curves (which are in correspondence with the
curves (which are in correspondence with the  -handles). We obtain a relation for each
-handles). We obtain a relation for each  -handle (which are in correspondence with the
-handle (which are in correspondence with the  curves). The
curves). The  curves describe the attaching maps of the
curves describe the attaching maps of the  -handles; thus we can compute
-handles; thus we can compute 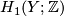 and
and 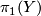 by investigating the intersections of the
by investigating the intersections of the  and
and  curves, as each intersection marks a
curves, as each intersection marks a  -handle attaching circle traveling geometrically once over a
-handle attaching circle traveling geometrically once over a  -handle.
-handle.
Let ![\gamma_{ij}=\gamma([\alpha_i],[\beta_j])](/images/math/1/e/9/1e9be0fff620893746fb6d430d6953c4.png) indicate the algebraic intersection of
indicate the algebraic intersection of 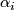 with
with 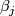 . Then
. Then ![H_1(Y;\mathbb{Z})\cong\langle x_1,\ldots, x_g\mid [x_i,x_j]\forall(i,j), \sum_{i=1}^g\gamma_{ij}x_i\forall j\rangle](/images/math/6/5/c/65c9d2bfb6315c384516c221c0bf0a2e.png) .
.
Now pick a basepoint 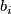 for each
for each 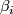 . Traveling once around
. Traveling once around 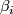 starting at
starting at 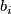 , say that
, say that 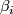 intersects
intersects 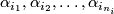 in order (with each entry indicating one intersection), with sign
in order (with each entry indicating one intersection), with sign 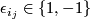 . Let
. Let 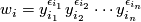 . Then
. Then 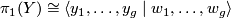 .
.
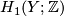 and
and 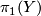 with group presentations, we can write the Hurewicz map
with group presentations, we can write the Hurewicz map 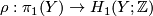 as the map
as the map ![\displaystyle \rho:\left\langle x_1,\ldots, x_g\mid [x_i,x_j]\forall(i,j), \sum_{i=1}^g\gamma_{ij}x_i\forall j\right\rangle\to\langle y_1,\ldots, y_g\mid w_1,\ldots, w_g\rangle](/images/math/a/f/3/af39ce0ad287fc00f87e0a5355cb6cb5.png)
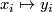 For each
For each 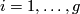 .
.