Talk:Circle actions on 3-manifolds (Ex)
(Difference between revisions)
(Created page with "<wikitex>; Insight: Try to quotient the manifold by the action. Note that you get something that looks kind of reasonable but isn't a manifold. Guess: The isotropy groups mus...") |
|||
| Line 2: | Line 2: | ||
Insight: Try to quotient the manifold by the action. Note that you get something that looks kind of reasonable but isn't a manifold. | Insight: Try to quotient the manifold by the action. Note that you get something that looks kind of reasonable but isn't a manifold. | ||
| − | Guess: The isotropy groups must all be the same. Consider a point, then the isotropy groups of its neighborhood are the same as | + | Guess: The isotropy groups must all be the same. Consider a point, then the isotropy groups of its neighborhood are the same as the point's. Consider the same method for a point on the boundary of an (open) region of fixed isotropy groups; this shows the set with identical isotropy groups is both open and closed. Then, the isotropy groups must in fact be $Z_n$. Then turn the $S^1$ action into one with trivial isotropy groups. Now try to take a cross section (how?). |
</wikitex> | </wikitex> | ||
Revision as of 07:19, 9 January 2019
Insight: Try to quotient the manifold by the action. Note that you get something that looks kind of reasonable but isn't a manifold.
Guess: The isotropy groups must all be the same. Consider a point, then the isotropy groups of its neighborhood are the same as the point's. Consider the same method for a point on the boundary of an (open) region of fixed isotropy groups; this shows the set with identical isotropy groups is both open and closed. Then, the isotropy groups must in fact be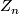 
. Then turn the 
action into one with trivial isotropy groups. Now try to take a cross section (how?).
