Talk:Bundle structures and lifting problems (Ex)
Exercise 2.1
Assume that there exists a lift 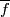 :
: 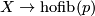 of
of  .
Then there exist maps
.
Then there exist maps  :
: 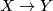 and
and 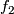 :
: ![X\times[0,1]\to Z](/images/math/5/c/d/5cdbcbe836ed7d107a7955e49b24c31d.png) such that for all
such that for all 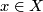 we have
we have 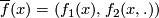 .
Since
.
Since 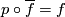 we find that
we find that 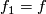 .
Furthermore we have for all
.
Furthermore we have for all 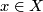 :
: 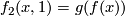 and
and 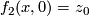 .
Thus
.
Thus 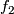 defines a homotopy from
defines a homotopy from 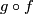 to a constant map.
to a constant map.
Assume that there exists  :
: ![X\times[0,1]\to Z](/images/math/5/c/d/5cdbcbe836ed7d107a7955e49b24c31d.png) such that for all
such that for all 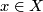 we have
we have 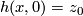 and
and 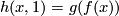 .
Define
.
Define 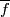 :
: 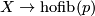 by
by 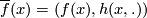 .
By the definitions of
.
By the definitions of  and of
and of 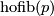 we find that
we find that 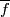 is well defined and a lift of
is well defined and a lift of  .
.
Exercise 4.1
The map $P(K(n+1,\mathbb{Z}/2\mathbb{Z}))\to K(n+1,\mathbb{Z}/2\mathbb{Z})$ is given by $\gamma\mapsto\gamma(1)$. Since $P(K(n+1,\mathbb{Z}/2\mathbb{Z}))$ is contractible, every third term in the long exact sequence in homotopy is zero. Thus we obtain for all $m\geq1$ that $\pi_m(K(n+1,\mathbb{Z}/2\mathbb{Z}))\cong\pi_{m-1}(\Omega K(n+1,\mathbb{Z}/2\mathbb{Z}))$. By the uniqueness of Eilenberg-MacLane spaces the assertion follows.