Talk:Bundle structures and lifting problems (Ex)
(Difference between revisions)
| Line 17: | Line 17: | ||
Since $P(K(n+1,\mathbb{Z}/2\mathbb{Z}))$ is contractible, every third term in the long exact sequence in homotopy is zero. | Since $P(K(n+1,\mathbb{Z}/2\mathbb{Z}))$ is contractible, every third term in the long exact sequence in homotopy is zero. | ||
Thus we obtain for all $m\geq1$ that $\pi_m(K(n+1,\mathbb{Z}/2\mathbb{Z}))\cong\pi_{m-1}(\Omega K(n+1,\mathbb{Z}/2\mathbb{Z}))$. | Thus we obtain for all $m\geq1$ that $\pi_m(K(n+1,\mathbb{Z}/2\mathbb{Z}))\cong\pi_{m-1}(\Omega K(n+1,\mathbb{Z}/2\mathbb{Z}))$. | ||
| − | By the uniqueness of Eilenberg-MacLane spaces the assertion follows. | + | By the uniqueness of Eilenberg-MacLane spaces the first assertion follows. |
| + | |||
| + | It is clear that composition of paths induces a group structure on $[Y,\Omega X]$. | ||
</wikitex> | </wikitex> | ||
Revision as of 19:24, 2 April 2012
Exercise 2.1
Assume that there exists a lift 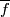 :
: 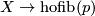 of
of  .
Then there exist maps
.
Then there exist maps  :
: 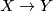 and
and  :
: ![X\times[0,1]\to Z](/images/math/5/c/d/5cdbcbe836ed7d107a7955e49b24c31d.png) such that for all
such that for all 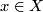 we have
we have 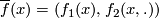 .
Since
.
Since 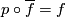 we find that
we find that 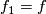 .
Furthermore we have for all
.
Furthermore we have for all 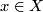 :
: 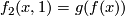 and
and 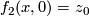 .
Thus
.
Thus  defines a homotopy from
defines a homotopy from 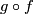 to a constant map.
to a constant map.
Assume that there exists  :
: ![X\times[0,1]\to Z](/images/math/5/c/d/5cdbcbe836ed7d107a7955e49b24c31d.png) such that for all
such that for all 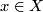 we have
we have 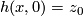 and
and 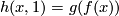 .
Define
.
Define 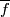 :
: 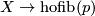 by
by 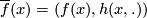 .
By the definitions of
.
By the definitions of  and of
and of 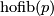 we find that
we find that 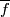 is well defined and a lift of
is well defined and a lift of  .
.
Exercise 4.1
The map 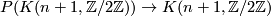 is given by
is given by 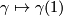 .
Since
.
Since 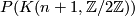 is contractible, every third term in the long exact sequence in homotopy is zero.
Thus we obtain for all
is contractible, every third term in the long exact sequence in homotopy is zero.
Thus we obtain for all 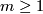 that
that 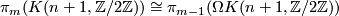 .
By the uniqueness of Eilenberg-MacLane spaces the first assertion follows.
.
By the uniqueness of Eilenberg-MacLane spaces the first assertion follows.
It is clear that composition of paths induces a group structure on ![[Y,\Omega X]](/images/math/3/d/3/3d36331b6ffc21a47fc28e20effd0b46.png) .
.