Talk:Bundle structures and lifting problems (Ex)
(Difference between revisions)
(Created page with "<wikitex>; '''Exercise 2.1''' Assume that there exists a lift $\overline{f}$: $X\to\mathrm{hofib}(p)$ of $f$. Then there exist maps $f_1$: $X\to Y$ and $f_2$: $X\times[0,1]\...") |
|||
| Line 7: | Line 7: | ||
Furthermore we have for all $x\in X$: $f_2(x,1)=g(f(x))$ and $f_2(x,0)=z_0$. | Furthermore we have for all $x\in X$: $f_2(x,1)=g(f(x))$ and $f_2(x,0)=z_0$. | ||
Thus $f_2$ defines a homotopy from $g\circ f$ to a constant map. | Thus $f_2$ defines a homotopy from $g\circ f$ to a constant map. | ||
| + | |||
| + | Assume that there exists $h$: $X\times[0,1]\to Z$ such that for all $x\in X$ we have $h(x,0)=z_0$ and $h(x,1)=g(f(x))$. | ||
| + | Define $\overline{f}$: $X\to\mathrm{hofib}(p)$ by $\overline{f}(x)=(f(x),h(x,.))$. | ||
| + | By the definitions of $h$ and of $\mathrm{hofib}(p)$ we find that $\overline{f}$ is well defined and a lift of $f$. | ||
</wikitex> | </wikitex> | ||
Revision as of 19:12, 2 April 2012
Exercise 2.1
Assume that there exists a lift 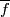 :
: 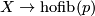 of
of  .
Then there exist maps
.
Then there exist maps  :
: 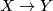 and
and 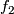 :
: ![X\times[0,1]\to Z](/images/math/5/c/d/5cdbcbe836ed7d107a7955e49b24c31d.png) such that for all
such that for all 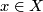 we have
we have 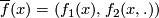 .
Since
.
Since 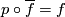 we find that
we find that 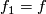 .
Furthermore we have for all
.
Furthermore we have for all 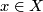 :
: 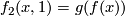 and
and 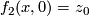 .
Thus
.
Thus 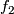 defines a homotopy from
defines a homotopy from 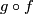 to a constant map.
to a constant map.
Assume that there exists  :
: ![X\times[0,1]\to Z](/images/math/5/c/d/5cdbcbe836ed7d107a7955e49b24c31d.png) such that for all
such that for all 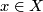 we have
we have 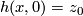 and
and 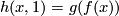 .
Define
.
Define 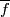 :
: 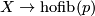 by
by 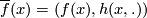 .
By the definitions of
.
By the definitions of  and of
and of 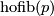 we find that
we find that 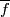 is well defined and a lift of
is well defined and a lift of  .
.