Talk:Betti numbers of 3-manifolds (Ex)
From Manifold Atlas
(Difference between revisions)
(Created page with "<wikitex>; Now let $M$ be a closed, orientable $3$-manifold with $\pi_1(M)=G$. View $M$ as a finite CW complex, with cells in dimensions-$0,1,2,3$, as usual. Attach cells of ...") |
m |
||
| Line 4: | Line 4: | ||
Thus, $b_1(G)=\text{rk} H_1(N;\mathbb{Z})=\text{rk}H_1(M;\mathbb{Z})=\text{rk}H_2(M;\mathbb{Z})\ge \text{rk} H_2(N;\mathbb{Z})=b_2(G)$, so $b_1(G)\ge b_2(G)$. | Thus, $b_1(G)=\text{rk} H_1(N;\mathbb{Z})=\text{rk}H_1(M;\mathbb{Z})=\text{rk}H_2(M;\mathbb{Z})\ge \text{rk} H_2(N;\mathbb{Z})=b_2(G)$, so $b_1(G)\ge b_2(G)$. | ||
| − | |||
| − | |||
| − | |||
</wikitex> | </wikitex> | ||
| − | |||
| − | |||
Latest revision as of 07:06, 8 January 2019
Now let  be a closed, orientable
be a closed, orientable  -manifold with
-manifold with 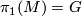 . View
. View  as a finite CW complex, with cells in dimensions-
as a finite CW complex, with cells in dimensions-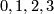 , as usual. Attach cells of dimension
, as usual. Attach cells of dimension 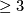 to
to  to obtain
to obtain  , a
, a 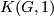 space. Then
space. Then 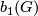 is the rank of
is the rank of 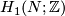 and
and 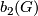 is the rank of
is the rank of 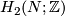 . By construction of
. By construction of  ,
, 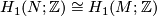 and the rank of
and the rank of 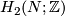 is bounded above by the rank of
is bounded above by the rank of 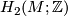 . Moreover,
. Moreover,  is a
is a  -manifold, so Poincaré duality says the ranks of
-manifold, so Poincaré duality says the ranks of 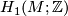 and
and 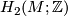 agree.
agree.
Thus, 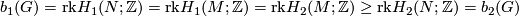 , so
, so 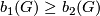 .
.
 -manifold with
-manifold with 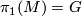 . View
. View  as a finite CW complex, with cells in dimensions-
as a finite CW complex, with cells in dimensions-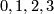 , as usual. Attach cells of dimension
, as usual. Attach cells of dimension 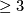 to
to  to obtain
to obtain  , a
, a 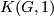 space. Then
space. Then 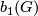 is the rank of
is the rank of 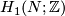 and
and 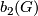 is the rank of
is the rank of 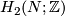 . By construction of
. By construction of  ,
, 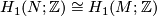 and the rank of
and the rank of 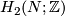 is bounded above by the rank of
is bounded above by the rank of 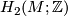 . Moreover,
. Moreover,  is a
is a  -manifold, so Poincaré duality says the ranks of
-manifold, so Poincaré duality says the ranks of 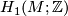 and
and 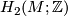 agree.
agree.
Thus, 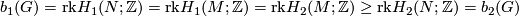 , so
, so 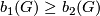 .
.