Talk:Betti numbers of 3-manifolds (Ex)
From Manifold Atlas
Now let  be a closed, orientable
be a closed, orientable  -manifold with
-manifold with 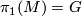 . View
. View  as a finite CW complex, with cells in dimensions-
as a finite CW complex, with cells in dimensions-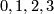 , as usual. Attach cells of dimension
, as usual. Attach cells of dimension 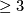 to
to  to obtain
to obtain  , a
, a 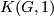 space. Then
space. Then 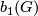 is the rank of
is the rank of 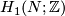 and
and 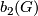 is the rank of
is the rank of 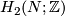 . By construction of
. By construction of  ,
, 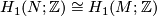 and the rank of
and the rank of 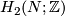 is bounded above by the rank of
is bounded above by the rank of 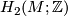 . Moreover,
. Moreover,  is a
is a  -manifold, so Poincaré duality says the ranks of
-manifold, so Poincaré duality says the ranks of 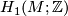 and
and 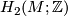 agree.
agree.
Thus, 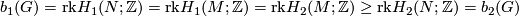 , so
, so 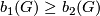 .
.