Surgery obstruction groups
(Difference between revisions)
(→Introduction) |
(→Introduction) |
||
| Line 3: | Line 3: | ||
== Introduction == | == Introduction == | ||
<wikitex>; | <wikitex>; | ||
| − | The surgery obstruction groups $L_n(\bZ\pi, w)$ of C.T.C. Wall \cite{Wall1999}, \cite{Wall1976} contain the obstructions to doing surgery on a degree 1 [[normal map]] $(f,b)\colon M \to X$ to obtain a homotopy equivalence. In this setting, $X$ is an $n$-dimensional Poincar\'e complex $\pi = \pi_1(X, x_0)$ is the fundamental group of $X$, and $w = w_1(X)$ is the first Stiefel-Whitney class. A homotopy equivalence $f\colon M \to X$ has a [[Whitehead torsion]] $\tau(f) \in Wh(\pi)$. The surgery obstruction groups for surgery up to a homotopy equivalence in a prescribed subgroup $U \ | + | The surgery obstruction groups $L_n(\bZ\pi, w)$ of C.T.C. Wall \cite{Wall1999}, \cite{Wall1976} contain the obstructions to doing surgery on a degree 1 [[normal map]] $(f,b)\colon M \to X$ to obtain a homotopy equivalence. In this setting, $X$ is an $n$-dimensional Poincar\'e complex $\pi = \pi_1(X, x_0)$ is the fundamental group of $X$, and $w = w_1(X)$ is the first Stiefel-Whitney class. A homotopy equivalence $f\colon M \to X$ has a [[Whitehead torsion]] $\tau(f) \in Wh(\pi)$. The surgery obstruction groups for surgery up to a homotopy equivalence with torsion in a prescribed subgroup $U \subseeqt Wh(\pi)$ are denoted $L^U_n(\bZ, w)$. The most important cases for geometric applications are $U = \{ 0 \}$, denoted $L^s_n(\bZ, w)$, or $U = Wh(\pi)$, denoted $L^h_n(\bZ, w)$. |
The surgery obstuctions groups $L_n(R\pi, w)$ depend on a coefficient ring $R$, a discrete group $\pi$ and an orientation character $w\colon \pi \to \{\pm 1\}$. In general the surgery obstruction groups are abelian groups. For finite groups $\pi$ the $L$-groups are finitely-generated and the only torsion is $2$-primary. | The surgery obstuctions groups $L_n(R\pi, w)$ depend on a coefficient ring $R$, a discrete group $\pi$ and an orientation character $w\colon \pi \to \{\pm 1\}$. In general the surgery obstruction groups are abelian groups. For finite groups $\pi$ the $L$-groups are finitely-generated and the only torsion is $2$-primary. | ||
Revision as of 16:16, 8 June 2010
|
The user responsible for this page is Hambleton. No other user may edit this page at present. |
|
This page has not been refereed. The information given here might be incomplete or provisional. |
1 Introduction
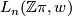 of C.T.C. Wall [Wall1999], [Wall1976] contain the obstructions to doing surgery on a degree 1 normal map
of C.T.C. Wall [Wall1999], [Wall1976] contain the obstructions to doing surgery on a degree 1 normal map 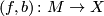 to obtain a homotopy equivalence. In this setting,
to obtain a homotopy equivalence. In this setting,  is an
is an  -dimensional Poincar\'e complex
-dimensional Poincar\'e complex 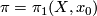 is the fundamental group of
is the fundamental group of  , and
, and 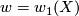 is the first Stiefel-Whitney class. A homotopy equivalence
is the first Stiefel-Whitney class. A homotopy equivalence 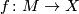 has a Whitehead torsion
has a Whitehead torsion 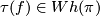 . The surgery obstruction groups for surgery up to a homotopy equivalence with torsion in a prescribed subgroup
. The surgery obstruction groups for surgery up to a homotopy equivalence with torsion in a prescribed subgroup Tex syntax errorare denoted
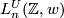 . The most important cases for geometric applications are
. The most important cases for geometric applications are 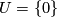 , denoted
, denoted 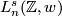 , or
, or 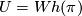 , denoted
, denoted 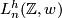 .
.
The surgery obstuctions groups 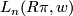 depend on a coefficient ring
depend on a coefficient ring  , a discrete group
, a discrete group  and an orientation character
and an orientation character 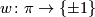 . In general the surgery obstruction groups are abelian groups. For finite groups
. In general the surgery obstruction groups are abelian groups. For finite groups  the
the  -groups are finitely-generated and the only torsion is
-groups are finitely-generated and the only torsion is  -primary.
-primary.
A Guide to the Calculation of Surgery Obstruction Groups, Hambleton & Taylor (2000), pp. 1-3
On the classification of hermitian forms: VI Group Rings, Wall (1976), pp. 1-2
2 References
- [Wall1976] C. T. C. Wall, Classification of Hermitian Forms. VI. Group rings, Ann. of Math. (2) 103 (1976), no.1, 1–80. MR0432737 (55 #5720) Zbl 0328.18006
- [Wall1999] C. T. C. Wall, Surgery on compact manifolds, American Mathematical Society, Providence, RI, 1999. MR1687388 (2000a:57089) Zbl 0935.57003