Steenrod problem
(Difference between revisions)
Haggai Tene (Talk | contribs) (Created page with "<!-- COMMENT: To achieve a unified layout, along with using the template below, please OBSERVE the following: besides, $...$ and $$...$$, you should use two environments: - Fo...") |
Haggai Tene (Talk | contribs) |
||
| Line 15: | Line 15: | ||
<wikitex>; | <wikitex>; | ||
| − | Given a space X there is a homomorphism | + | Given a space X, there is a homomorphism $\Phi : \Omega^{SO}_{∗}(X) \to H_{*}(X,\mathbb{Z})$, called the Thom homomorphism, given by $[M,f] \to f_{*}([M])$ where $[M]$ is the fundamental class of $M$. The elements in the image of $\Phi$ are called representable. |
| − | In certain situations it is convenient to assume that a homology class is | + | In certain situations it is convenient to assume that a homology class is representable. In dimensions $0$ and $1$ it is clear that $\Phi$ is surjective (even an isomorphism). It is less obvious in dimension $2$, but also can be shown geometrically. This made Steenrod raise his famous problem in 1946 <ref>Insert footnote text here</ref>: |
| − | Given a simplicial complex X, is every (integral) homology class representable? | + | Given a simplicial complex $X$, is every (integral) homology class representable? |
</wikitex> | </wikitex> | ||
Revision as of 12:18, 31 March 2011
|
This page has not been refereed. The information given here might be incomplete or provisional. |
1 Introduction
Given a space X, there is a homomorphism 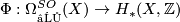 , called the Thom homomorphism, given by
, called the Thom homomorphism, given by ![[M,f] \to f_{*}([M])](/images/math/c/7/1/c711fc19bedc6bd184836dcdf7eb3273.png) where
where ![[M]](/images/math/f/a/0/fa08c3d5d2f54260952acc8a646b5025.png) is the fundamental class of
is the fundamental class of  . The elements in the image of
. The elements in the image of 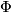 are called representable.
In certain situations it is convenient to assume that a homology class is representable. In dimensions
are called representable.
In certain situations it is convenient to assume that a homology class is representable. In dimensions  and
and  it is clear that
it is clear that 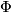 is surjective (even an isomorphism). It is less obvious in dimension
is surjective (even an isomorphism). It is less obvious in dimension  , but also can be shown geometrically. This made Steenrod raise his famous problem in 1946 [1];:
Given a simplicial complex
, but also can be shown geometrically. This made Steenrod raise his famous problem in 1946 [1];:
Given a simplicial complex  , is every (integral) homology class representable?
, is every (integral) homology class representable?
2 References
Cite error:
<ref> tags exist, but no <references/> tag was found