Steenrod problem
|
This page has not been refereed. The information given here might be incomplete or provisional. |
[edit] 1 Introduction
Given a space X, there is a homomorphism 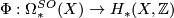 , called the Thom homomorphism, given by
, called the Thom homomorphism, given by ![[M,f] \to f_{*}([M])](/images/math/c/7/1/c711fc19bedc6bd184836dcdf7eb3273.png) where
where ![[M]](/images/math/f/a/0/fa08c3d5d2f54260952acc8a646b5025.png) is the fundamental class of
is the fundamental class of  . The elements in the image of
. The elements in the image of 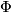 are called representable.
In certain situations it is convenient to assume that a homology class is representable. In dimensions
are called representable.
In certain situations it is convenient to assume that a homology class is representable. In dimensions  and
and  it is clear that
it is clear that 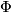 is surjective (even an isomorphism). It is less obvious in dimension
is surjective (even an isomorphism). It is less obvious in dimension  , but also can be shown geometrically. This made Steenrod raise his famous problem in 1946 [Eilenberg1949]:
, but also can be shown geometrically. This made Steenrod raise his famous problem in 1946 [Eilenberg1949]:
Given a simplicial complex  , is every (integral) homology class representable?
, is every (integral) homology class representable?
The answer was given by Thom in 1954 [Thom1954]. He showed that in dimensions 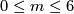 this is true but in general this is not the case. He constructed a counter example in dimension
this is true but in general this is not the case. He constructed a counter example in dimension 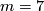 . Thom also showed that the corresponding problem with
. Thom also showed that the corresponding problem with 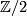 coefficients is correct, that is the corresponding homomorphism
coefficients is correct, that is the corresponding homomorphism 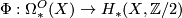 is surjective.
Thom also proved the following:
is surjective.
Thom also proved the following:
Theorem 1.1 [Thom1954, Theorem III.4].
For every class in dimension  of integral homology of a finite polyhedron K, there exists a non zero integer
of integral homology of a finite polyhedron K, there exists a non zero integer  which depends only on p, such that the product
which depends only on p, such that the product 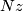 is the image of the fundamental class of a closed oriented differentiable manifold.
is the image of the fundamental class of a closed oriented differentiable manifold.
More about that can be found in [Sullivan2004].
[edit] 2 References
- [Eilenberg1949] S. Eilenberg, On the problems of topology, Ann. of Math. (2) 50 (1949), 247–260. MR0030189 (10,726b) Zbl 0034.25304
- [Sullivan2004] D. Sullivan, René Thom's work on geometric homology and bordism, Bull. Amer. Math. Soc. (N.S.) 41 (2004), no.3, 341–350 (electronic). MR2058291 Zbl 1045.57001
- [Thom1954] R. Thom, Quelques propriétés globales des variétés différentiables, Comment. Math. Helv. 28 (1954), 17–86. MR0061823 (15,890a) Zbl 0057.15502