Spivak normal fibration (Ex)
m |
m |
||
| Line 3: | Line 3: | ||
{{beginthm|Exercise}} | {{beginthm|Exercise}} | ||
| − | Let $(M, \partial M)$ be a compact, connected, oriented, $n$-dimensional manifold with boundary, embedded in $ | + | Let $(M, \partial M)$ be a compact, connected, oriented, $n$-dimensional manifold with boundary, embedded in the $n$-sphere $S^n$. The collapse map $c:S^n\to M/\partial M$ is defined by |
$$c(x)=\begin{cases} x&\text{if }x\in M-\partial M\\\{\partial M\}&\text{else}\end{cases}$$ | $$c(x)=\begin{cases} x&\text{if }x\in M-\partial M\\\{\partial M\}&\text{else}\end{cases}$$ | ||
Let $h:\pi_n(M, \partial M)\to H_n(M, \partial M)$ be the [[Hurewicz homomorphism]], show that | Let $h:\pi_n(M, \partial M)\to H_n(M, \partial M)$ be the [[Hurewicz homomorphism]], show that | ||
Revision as of 07:39, 30 May 2012
In the following exercises  is a connected Poincaré complex of formal dimension
is a connected Poincaré complex of formal dimension  and
and  is a compact manifold of dimension
is a compact manifold of dimension  .
.
Exercise 0.1.
Let 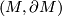 be a compact, connected, oriented,
be a compact, connected, oriented,  -dimensional manifold with boundary, embedded in the
-dimensional manifold with boundary, embedded in the  -sphere
-sphere  . The collapse map
. The collapse map 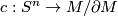 is defined by
is defined by
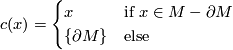
Let 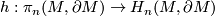 be the Hurewicz homomorphism, show that
be the Hurewicz homomorphism, show that
![\displaystyle h([c])=\pm [M,\partial M]](/images/math/2/e/3/2e3fa87f344c35e33af28fa205bdcead.png)
Exercise 0.2.
Let 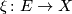 be a spherical fibration
be a spherical fibration  with homotopy fibre
with homotopy fibre 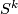 . Show that
. Show that  is homotopy equivalent to a Poincaré complex of formal dimension
is homotopy equivalent to a Poincaré complex of formal dimension  .
.
Here is an interesting problem we now confront
Problem 0.3.
Determine the Spivak normal fibration of  above in terms of
above in terms of  and the Spivak normal fibration of
and the Spivak normal fibration of  .
.
Here are some hints for this problem: Tangent bundles of bundles (Ex), [Wall1966a], [Chazin1975]
Remark 0.4. Exercise 0.2 is a diffcult problem. It was solved in greater generality in [Klein2001a, Theorem I].