Some calculations involving configuration spaces of distinct points
m |
(→Introduction) |
||
| Line 3: | Line 3: | ||
<wikitex>; | <wikitex>; | ||
‘The complement of the diagonal’ and ‘the Gauss map’ ideas play a great role in different branches of mathematics<!-- [Gl68, Va92]-->. The Haefliger-Wu invariant is a manifestation of these ideas in the theory of embeddings. The complement to the diagonal idea originated from two celebrated theorems: the Lefschetz Fixed Point Theorem and the Borsuk-Ulam Antipodes Theorem. | ‘The complement of the diagonal’ and ‘the Gauss map’ ideas play a great role in different branches of mathematics<!-- [Gl68, Va92]-->. The Haefliger-Wu invariant is a manifestation of these ideas in the theory of embeddings. The complement to the diagonal idea originated from two celebrated theorems: the Lefschetz Fixed Point Theorem and the Borsuk-Ulam Antipodes Theorem. | ||
| + | |||
| + | In introducing notation and definitions we follow [https://www.mccme.ru/circles/oim/eliminat_talk.pdf slides by A. Skopenkov] | ||
The ''deleted product'' | The ''deleted product'' | ||
| Line 8: | Line 10: | ||
This is the configuration space of ordered pairs of distinct points of $K$. | This is the configuration space of ordered pairs of distinct points of $K$. | ||
| − | Suppose that $f:K\to\R^ | + | Suppose that $f:K\to\R^m$ is an embedding of a subset $K\subset \mathbb R^n$. |
| − | Then the map $\widetilde f:\widetilde K\to S^{ | + | Then the map $\widetilde f:\widetilde K\to S^{m-1}$ is well-defined by the Gauss formula |
$$\widetilde f(x,y)=\frac{f(x)-f(y)}{|f(x)-f(y)|}.$$ | $$\widetilde f(x,y)=\frac{f(x)-f(y)}{|f(x)-f(y)|}.$$ | ||
We have $\widetilde f(y,x)=-\widetilde f(x,y)$, i.e. this map is equivariant with respect to the `exchanging factors' involution | We have $\widetilde f(y,x)=-\widetilde f(x,y)$, i.e. this map is equivariant with respect to the `exchanging factors' involution | ||
| − | $(x,y)\mapsto(y,x)$ on $\widetilde K$ and the antipodal involution on $S^{ | + | $(x,y)\mapsto(y,x)$ on $\widetilde K$ and the antipodal involution on $S^{m-1}$. |
| − | Thus the existence of an equivariant map $\widetilde K\to S^{ | + | Thus the existence of an equivariant map $\widetilde K\to S^{m-1}$ is a necessary condition for the embeddability of $K$ in $\R^m$. |
| − | {{ | + | Denote by $\mathrm{Emb}^{m}K$ the set embeddings of $K$ into $\mathbb R^{m}$ up to isotopy. |
| − | + | Let $\pi_{\mathrm{eq}}^{m}(K) = [K;S^{m}]_{\mathrm{eq}}$ be the set of equivariant maps ̃$K\to S^m$ up to equivariant homotopy. | |
| − | + | ||
| − | + | <!--Definition of the Haefliger-Wu invariant $\alpha$--> | |
| − | + | ||
| − | + | '''The Haefliger-Wu invariant''' | |
| + | $\alpha:\mathrm{Emb}^{m}K\to \pi_{\mathrm{eq}}^{m-1}(\widetilde{K})$ | ||
| + | is induced by the Gauss map. | ||
| + | I.e. $\alpha([f]) = [\widetilde f]$. | ||
| + | <!-- The Haefliger-Wu invariant and the Gauss map are analogously defined for $N_0$; we will denote them by $\alpha_0$ in this case.--> | ||
{{beginthm|Theorem}} | {{beginthm|Theorem}} | ||
The Haefliger-Wu invariant $\alpha:\mathrm{Emb}^m K\to\pi^{m-1}_{\mathrm{eq}}( \widetilde K)$ is one-to-one for $2m\ge 3n+4$. | The Haefliger-Wu invariant $\alpha:\mathrm{Emb}^m K\to\pi^{m-1}_{\mathrm{eq}}( \widetilde K)$ is one-to-one for $2m\ge 3n+4$. | ||
{{endthm}} | {{endthm}} | ||
| + | |||
| + | See \cite[$\S$ 5]{Skopenkov2006} and \cite[6.4]{Haefliger1963}, \cite[Theorem 1.1$\alpha\partial$]{Skopenkov2002} for the DIFF case and \cite[Theorem 1.3$\alpha\partial$]{Skopenkov2002} for the PL case. | ||
</wikitex> | </wikitex> | ||
Revision as of 12:44, 9 April 2020
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
‘The complement of the diagonal’ and ‘the Gauss map’ ideas play a great role in different branches of mathematics. The Haefliger-Wu invariant is a manifestation of these ideas in the theory of embeddings. The complement to the diagonal idea originated from two celebrated theorems: the Lefschetz Fixed Point Theorem and the Borsuk-Ulam Antipodes Theorem.
In introducing notation and definitions we follow slides by A. Skopenkov
The deleted product
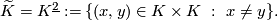
This is the configuration space of ordered pairs of distinct points of  .
.
Suppose that 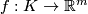 is an embedding of a subset
is an embedding of a subset 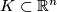 .
Then the map
.
Then the map 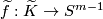 is well-defined by the Gauss formula
is well-defined by the Gauss formula
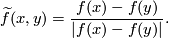
We have 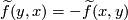 , i.e. this map is equivariant with respect to the `exchanging factors' involution
, i.e. this map is equivariant with respect to the `exchanging factors' involution
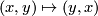 on
on 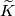 and the antipodal involution on
and the antipodal involution on 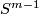 .
Thus the existence of an equivariant map
.
Thus the existence of an equivariant map 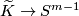 is a necessary condition for the embeddability of
is a necessary condition for the embeddability of  in
in  .
.
Denote by 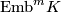 the set embeddings of
the set embeddings of  into
into 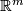 up to isotopy.
Let
up to isotopy.
Let ![\pi_{\mathrm{eq}}^{m}(K) = [K;S^{m}]_{\mathrm{eq}}](/images/math/d/6/5/d65b78e9c5a0765100818a1be03dcbe8.png) be the set of equivariant maps ̃
be the set of equivariant maps ̃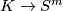 up to equivariant homotopy.
up to equivariant homotopy.
The Haefliger-Wu invariant
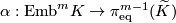 is induced by the Gauss map.
I.e.
is induced by the Gauss map.
I.e. ![\alpha([f]) = [\widetilde f]](/images/math/d/f/6/df6dfc7ac8fc6b0d2cf4062da4537b6b.png) .
.
Theorem 1.1.
The Haefliger-Wu invariant 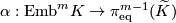 is one-to-one for
is one-to-one for 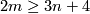 .
.
See [Skopenkov2006,  5] and [Haefliger1963, 6.4], [Skopenkov2002, Theorem 1.1
5] and [Haefliger1963, 6.4], [Skopenkov2002, Theorem 1.1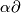 ] for the DIFF case and [Skopenkov2002, Theorem 1.3
] for the DIFF case and [Skopenkov2002, Theorem 1.3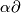 ] for the PL case.
] for the PL case.
2 Uniqueness theorems
Lemma 2.1.
Assume that  is a compact
is a compact  -manifold and either
-manifold and either
(a) 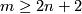 or
or
(b)  is connected and
is connected and 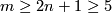 .
.
Then every two every two equivariant maps 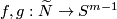 are equivariantly homotopic.
are equivariantly homotopic.
Proof.
Take an arbitrary equivariant triangulation  of
of 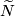 .
.
(a) One can easily construct an equivariant homotopy between restrictions of  and
and  on vertices of
on vertices of  .
By general position a homotopy of
.
By general position a homotopy of 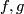 on the boundary of a
on the boundary of a  -simplex can be extended to a homotopy on the whole
-simplex can be extended to a homotopy on the whole  -simplex since
-simplex since 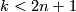 .
We extend equivariant homotopy on symmetric simplices in the symmetric way, so we obtain an equivariant homotopy.
.
We extend equivariant homotopy on symmetric simplices in the symmetric way, so we obtain an equivariant homotopy.
(b) Since 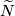 has non-empty boundary, there exists an equivariant deformational retraction of
has non-empty boundary, there exists an equivariant deformational retraction of 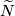 to an equivariant
to an equivariant 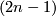 -subcomplex of
-subcomplex of  . A homotopy on the subcomplex can by constructed similarly to case~(a). This homotopy can be extended to a homotopy on
. A homotopy on the subcomplex can by constructed similarly to case~(a). This homotopy can be extended to a homotopy on 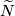 .
QED
.
QED
3 Invariants
...
4 Classification/Characterization
...
5 Further discussion
...
6 References
- [Haefliger1963] A. Haefliger, Plongements différentiables dans le domain stable., Comment. Math. Helv.37 (1963), 155-176.
- [Skopenkov2002] A. Skopenkov, On the Haefliger-Hirsch-Wu invariants for embeddings and immersions., Comment. Math. Helv. 77 (2002), no.1, 78-124. MRMR1898394 (2003c:57023) Zbl 1012.57035
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.