Some calculations involving configuration spaces of distinct points
m (→Introduction) |
(→Uniqueness theorems) |
||
| (14 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{Stub}} | {{Stub}} | ||
== Introduction == | == Introduction == | ||
<wikitex>; | <wikitex>; | ||
| − | ‘The complement of the diagonal’ and ‘the Gauss map’ ideas play a great role in different branches of mathematics<!-- [Gl68, Va92]-->. The Haefliger-Wu invariant is a manifestation of these ideas in the theory of embeddings. The complement to the diagonal idea originated from two celebrated theorems: the Lefschetz Fixed Point Theorem and the Borsuk-Ulam Antipodes Theorem. | + | ‘The complement of the diagonal’ and ‘the Gauss map’ ideas play a great role in different branches of mathematics<!-- [Gl68, Va92]-->. The Haefliger-Wu invariant is a manifestation of these ideas in the theory of embeddings. The complement to the diagonal idea originated from two celebrated theorems: the Lefschetz Fixed Point Theorem and the Borsuk-Ulam Antipodes Theorem. See \cite{Vassiliev1992}. |
| + | |||
| + | In introducing notation and definitions we follow \cite{Skopenkov2020a}. | ||
| + | |||
| + | If the category is omitted, then a result stated below holds in both the smooth and piecewise-linear (PL) category. | ||
The ''deleted product'' | The ''deleted product'' | ||
| Line 21: | Line 12: | ||
This is the configuration space of ordered pairs of distinct points of $K$. | This is the configuration space of ordered pairs of distinct points of $K$. | ||
| − | Suppose that $f:K\to\R^ | + | Suppose that $f:K\to\R^m$ is an embedding of a subset $K\subset \mathbb R^N$. |
| − | Then the map $\widetilde f:\widetilde K\to S^{ | + | Then the map $\widetilde f:\widetilde K\to S^{m-1}$ is well-defined by the Gauss formula |
$$\widetilde f(x,y)=\frac{f(x)-f(y)}{|f(x)-f(y)|}.$$ | $$\widetilde f(x,y)=\frac{f(x)-f(y)}{|f(x)-f(y)|}.$$ | ||
We have $\widetilde f(y,x)=-\widetilde f(x,y)$, i.e. this map is equivariant with respect to the `exchanging factors' involution | We have $\widetilde f(y,x)=-\widetilde f(x,y)$, i.e. this map is equivariant with respect to the `exchanging factors' involution | ||
| − | $(x,y)\mapsto(y,x)$ on $\widetilde K$ and the antipodal involution on $S^{ | + | $(x,y)\mapsto(y,x)$ on $\widetilde K$ and the antipodal involution on $S^{m-1}$. |
| − | Thus the existence of an equivariant map $\widetilde K\to S^{ | + | Thus the existence of an equivariant map $\widetilde K\to S^{m-1}$ is a necessary condition for the embeddability of $K$ in $\R^m$. |
| − | {{ | + | Denote by $\mathrm{Emb}^{m}K$ the set embeddings of $K$ into $\mathbb R^{m}$ up to isotopy. |
| − | + | Let $\pi_{\mathrm{eq}}^{m}(\widetilde K) = [\widetilde K;S^{m}]_{\mathrm{eq}}$ be the set of equivariant maps $\widetilde K \to S^m$ up to equivariant homotopy. By $[·]$ we denote the isotopy class of an embedding or the homotopy class of a map. | |
| − | + | ||
| − | + | <!--Definition of the Haefliger-Wu invariant $\alpha$--> | |
| − | + | '''The Haefliger-Wu invariant''' | |
| − | + | $\alpha:\mathrm{Emb}^{m}K\to \pi_{\mathrm{eq}}^{m-1}(\widetilde{K})$ is defined by formula | |
| + | <!--is induced by the Gauss map.--> | ||
| + | $\alpha([f]) = [\widetilde f]$. | ||
| + | <!-- The Haefliger-Wu invariant and the Gauss map are analogously defined for $N_0$; we will denote them by $\alpha_0$ in this case.--> | ||
{{beginthm|Theorem}} | {{beginthm|Theorem}} | ||
| − | The Haefliger-Wu invariant $\alpha:\mathrm{Emb}^m K\to\pi^{m-1}_{\mathrm{eq}}( \widetilde K)$ is one-to-one | + | The Haefliger-Wu invariant $\alpha:\mathrm{Emb}^m K\to\pi^{m-1}_{\mathrm{eq}}( \widetilde K)$ is one-to-one either |
| + | |||
| + | (a) $K$ is a compact connected $n$-complex and $2m\ge 3n+4$ or | ||
| + | |||
| + | <!--(b) $K$ is a compact connected $n$-manifold with nonempty boundary and $2m\ge 3n+4$ or--> | ||
| + | (b) $K$ is a compact $n$-manifold with nonempty boundary, $(K, \partial K)$ is $k$-connected, $\pi_1(\partial K) = 0$, | ||
| + | $k + 3 \le n$, $(n, k) \notin \{(5, 2), (4, 1)\}$ and $2m\ge 3n+2-k$. | ||
{{endthm}} | {{endthm}} | ||
| + | |||
| + | See \cite[$\S$ 5]{Skopenkov2006} and \cite[6.4]{Haefliger1963}, \cite[Theorem 1.1$\alpha\partial$]{Skopenkov2002} for the DIFF case and \cite[Theorem 1.3$\alpha\partial$]{Skopenkov2002} for the PL case. | ||
</wikitex> | </wikitex> | ||
| Line 49: | Line 51: | ||
(b) $N$ is connected and $m \ge 2n+1 \ge 5$. | (b) $N$ is connected and $m \ge 2n+1 \ge 5$. | ||
| − | Then | + | Then each two equivariant maps from $\widetilde N$ to $S^{m-1}$ are equivariantly homotopic. |
{{endthm}} | {{endthm}} | ||
| + | |||
| + | Hereafter denote by $\widetilde K$ the product $K\times K$ minus tubular neighborhood of the diagonal. | ||
''Proof.'' | ''Proof.'' | ||
| − | + | Given two equivariant maps $\phi, \psi\colon\widetilde N \to S^{m-1}$ take an arbitrary equivariant triangulation $T$ of $\widetilde N$. | |
| − | (a) One can easily construct an equivariant homotopy between restrictions of $ | + | (a) One can easily construct an equivariant homotopy between restrictions of $\phi$ and $\psi$ |
on vertices of $T$. | on vertices of $T$. | ||
| − | By general position a homotopy | + | By general position a homotopy between $\phi$ and $\psi$ on the boundary of a simplex can be extended to a homotopy on the whole simplex since the dimension of the simplex does not exceed $2n+1$. |
We extend equivariant homotopy on symmetric simplices in the symmetric way, so we obtain an equivariant homotopy. | We extend equivariant homotopy on symmetric simplices in the symmetric way, so we obtain an equivariant homotopy. | ||
| − | (b) Since $\widetilde{N}$ has non-empty boundary, there exists an equivariant deformational retraction of $\widetilde{N}$ to an equivariant $(2n-1)$-subcomplex of $T$. A homotopy on the subcomplex can by constructed similarly to case | + | (b) Since $\widetilde{N}$ has non-empty boundary, there exists an equivariant deformational retraction of $\widetilde{N}$ to an equivariant $(2n-1)$-subcomplex of $T$. A homotopy between $\phi$ and $\psi$ on the subcomplex can by constructed similarly to case (a). This homotopy can be extended to a homotopy on $\widetilde{N}$. |
QED | QED | ||
| + | |||
| + | {{beginthm|Lemma}}\label{th::unknotting} | ||
| + | Assume that $N$ is a closed $k$-connected $n$-manifold and $m-1 \ge 2n-k$. | ||
| + | |||
| + | Then each two equivariant maps from $\widetilde N$ to $S^{m-1}$ are equivariantly homotopic. | ||
| + | {{endthm}} | ||
</wikitex> | </wikitex> | ||
| − | == Invariants == | + | <!--== Invariants == |
<wikitex>; | <wikitex>; | ||
... | ... | ||
| Line 78: | Line 88: | ||
... | ... | ||
</wikitex> | </wikitex> | ||
| − | + | == Acknowledgments == | |
... | ... | ||
Latest revision as of 15:42, 8 January 2021
|
This page has not been refereed. The information given here might be incomplete or provisional. |
[edit] 1 Introduction
‘The complement of the diagonal’ and ‘the Gauss map’ ideas play a great role in different branches of mathematics. The Haefliger-Wu invariant is a manifestation of these ideas in the theory of embeddings. The complement to the diagonal idea originated from two celebrated theorems: the Lefschetz Fixed Point Theorem and the Borsuk-Ulam Antipodes Theorem. See [Vassiliev1992].
In introducing notation and definitions we follow [Skopenkov2020a].
If the category is omitted, then a result stated below holds in both the smooth and piecewise-linear (PL) category.
The deleted product
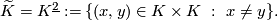
This is the configuration space of ordered pairs of distinct points of  .
.
Suppose that 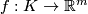 is an embedding of a subset
is an embedding of a subset 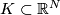 .
Then the map
.
Then the map 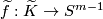 is well-defined by the Gauss formula
is well-defined by the Gauss formula
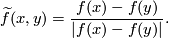
We have 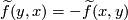 , i.e. this map is equivariant with respect to the `exchanging factors' involution
, i.e. this map is equivariant with respect to the `exchanging factors' involution
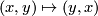 on
on  and the antipodal involution on
and the antipodal involution on 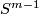 .
Thus the existence of an equivariant map
.
Thus the existence of an equivariant map 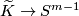 is a necessary condition for the embeddability of
is a necessary condition for the embeddability of  in
in  .
.
Denote by 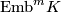 the set embeddings of
the set embeddings of  into
into 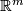 up to isotopy.
Let
up to isotopy.
Let ![\pi_{\mathrm{eq}}^{m}(\widetilde K) = [\widetilde K;S^{m}]_{\mathrm{eq}}](/images/math/8/d/a/8daa22f99319fe87dfc0028c51ae890a.png) be the set of equivariant maps
be the set of equivariant maps 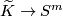 up to equivariant homotopy. By
up to equivariant homotopy. By ![[·]](/images/math/e/1/a/e1a16d717e4791077867654c63556327.png) we denote the isotopy class of an embedding or the homotopy class of a map.
we denote the isotopy class of an embedding or the homotopy class of a map.
The Haefliger-Wu invariant
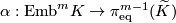 is defined by formula
is defined by formula
![\alpha([f]) = [\widetilde f]](/images/math/d/f/6/df6dfc7ac8fc6b0d2cf4062da4537b6b.png) .
.
Theorem 1.1.
The Haefliger-Wu invariant 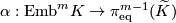 is one-to-one either
is one-to-one either
(a)  is a compact connected
is a compact connected  -complex and
-complex and 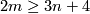 or
or
(b)  is a compact
is a compact  -manifold with nonempty boundary,
-manifold with nonempty boundary, 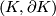 is
is  -connected,
-connected, 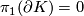 ,
,
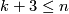 ,
, 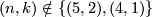 and
and 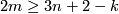 .
.
See [Skopenkov2006,  5] and [Haefliger1963, 6.4], [Skopenkov2002, Theorem 1.1
5] and [Haefliger1963, 6.4], [Skopenkov2002, Theorem 1.1 ] for the DIFF case and [Skopenkov2002, Theorem 1.3
] for the DIFF case and [Skopenkov2002, Theorem 1.3 ] for the PL case.
] for the PL case.
[edit] 2 Uniqueness theorems
Lemma 2.1.
Assume that  is a compact
is a compact  -manifold and either
-manifold and either
(a) 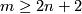 or
or
(b)  is connected and
is connected and 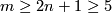 .
.
Then each two equivariant maps from 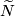 to
to 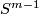 are equivariantly homotopic.
are equivariantly homotopic.
Hereafter denote by 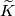 the product
the product 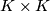 minus tubular neighborhood of the diagonal.
minus tubular neighborhood of the diagonal.
Proof.
Given two equivariant maps 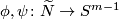 take an arbitrary equivariant triangulation
take an arbitrary equivariant triangulation  of
of 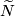 .
.
(a) One can easily construct an equivariant homotopy between restrictions of  and
and 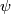 on vertices of
on vertices of  .
By general position a homotopy between
.
By general position a homotopy between  and
and 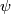 on the boundary of a simplex can be extended to a homotopy on the whole simplex since the dimension of the simplex does not exceed
on the boundary of a simplex can be extended to a homotopy on the whole simplex since the dimension of the simplex does not exceed 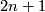 .
We extend equivariant homotopy on symmetric simplices in the symmetric way, so we obtain an equivariant homotopy.
.
We extend equivariant homotopy on symmetric simplices in the symmetric way, so we obtain an equivariant homotopy.
(b) Since 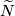 has non-empty boundary, there exists an equivariant deformational retraction of
has non-empty boundary, there exists an equivariant deformational retraction of 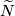 to an equivariant
to an equivariant 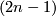 -subcomplex of
-subcomplex of  . A homotopy between
. A homotopy between  and
and 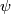 on the subcomplex can by constructed similarly to case (a). This homotopy can be extended to a homotopy on
on the subcomplex can by constructed similarly to case (a). This homotopy can be extended to a homotopy on 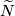 .
QED
.
QED
Lemma 2.2.
Assume that  is a closed
is a closed  -connected
-connected  -manifold and
-manifold and 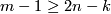 .
.
Then each two equivariant maps from 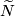 to
to 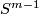 are equivariantly homotopic.
are equivariantly homotopic.
[edit] 3 References
- [Haefliger1963] A. Haefliger, Plongements différentiables dans le domain stable., Comment. Math. Helv.37 (1963), 155-176.
- [Skopenkov2002] A. Skopenkov, On the Haefliger-Hirsch-Wu invariants for embeddings and immersions., Comment. Math. Helv. 77 (2002), no.1, 78-124. MRMR1898394 (2003c:57023) Zbl 1012.57035
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2020a] https://www.mccme.ru/circles/oim/eliminat_talk.pdf
- [Vassiliev1992]
V. A. Vassiliev, Complements of discriminants of smooth maps: Topology and applications., Amer. Math. Soc., Providence, RI, (1992).