Simplicial volume
|
An earlier version of this page was published in the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 09:51, 1 April 2011 and the changes since publication. |
|
The user responsible for this page is Clara Löh. No other user may edit this page at present. |
Contents |
1 Definition and history
The simplicial volume is a homotopy invariant of oriented closed connected manifolds that was introduced by Gromov in his proof of Mostow rigidity [Munkholm1980][Gromov1982]. Intuitively, the simplicial volume measures how difficult it is to describe the manifold in question in terms of simplices (with real coefficients):
Definition (Simplicial volume) 1.1.
Let  be an oriented closed connected manifold of dimension
be an oriented closed connected manifold of dimension  .
Then the simplicial volume (also called Gromov norm) of
.
Then the simplicial volume (also called Gromov norm) of  is defined as
is defined as
![\displaystyle \|M\| := \bigl\| [M] \bigr\|_1 = \inf \bigl\{ |c|_1 \bigm| \text{$c \in C_n(M;\mathbb{R})$ is a fundamental cycle of $M$} \bigr\} \in \mathbb{R}_{\geq 0},](/images/math/c/2/2/c22511eadabaaaa5caa7565812d6977a.png)
where ![[M] \in H_n(M;\mathbb{R})](/images/math/7/d/7/7d74a20a6efc50970d884cfa1c1e5861.png) is the fundamental class of
is the fundamental class of  with real coefficients.
with real coefficients.
- Here,
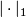 denotes the
denotes the  -norm on the singular chain complex
-norm on the singular chain complex 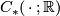 with real coefficients induced from the (unordered) basis given by all singular simplices, i.e.: for a topological space
with real coefficients induced from the (unordered) basis given by all singular simplices, i.e.: for a topological space Tex syntax error
and a chain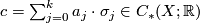 (in reduced form), the
(in reduced form), the  -norm of
-norm of  is given by
is given by
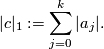
- Moreover,
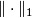 denotes the
denotes the  -semi-norm on singular homology
-semi-norm on singular homology 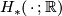 with real coefficients, which is induced by
with real coefficients, which is induced by 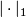 . More explicitly, if
. More explicitly, if Tex syntax error
is a topological space and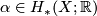 , then
, then
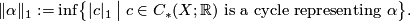
Convention 1.2. In the following, if not explicitly stated otherwise, all manifolds are topological manifolds and are of non-zero dimension.
2 Functoriality and elementary examples
The  -semi-norm is functorial in the following sense [Gromov1999]:
-semi-norm is functorial in the following sense [Gromov1999]:
Proposition (Functoriality of the  -semi-norm) 2.1.
If
-semi-norm) 2.1.
If 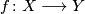 is a continuous map of topological spaces and
is a continuous map of topological spaces and 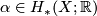 , then
, then
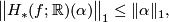
as can be seen by inspecting the definition of 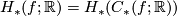 and of
and of 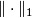 .
.
Corollary 2.2.
- Let
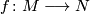 be a map of oriented closed connected manifolds of the same dimension. Then
be a map of oriented closed connected manifolds of the same dimension. Then
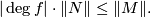
- Because homotopy equivalences of oriented closed connected manifolds have degree
 or
or  , it follows that the simplicial volume indeed is a homotopy invariant of oriented closed connected manifolds.
, it follows that the simplicial volume indeed is a homotopy invariant of oriented closed connected manifolds.
Hence, all oriented closed connected manifolds admitting a self-map of non-trivial degree (i.e., not equal to  ,
,  , or
, or  ) have vanishing simplicial volume; for instance, the simplicial volume of all
) have vanishing simplicial volume; for instance, the simplicial volume of all
- spheres
- tori
- (odd-dimensional) real projective spaces
- complex projective spaces
is zero.
3 "Computing" simplicial volume
In most cases, trying to compute the simplicial volume by inspecting the definition proves to be futile;
the two main sources for non-trivial estimates and inheritance properties of the simplicial volume are:
- Geometric: The connection between simplicial volume and Riemannian geometry (see below).
- Algebraic: The connection between simplicial volume and bounded cohomology (see below).
1 Simplicial volume and Riemannian geometry
A fascinating aspect of the simplicial volume is that it is a homotopy invariant encoding non-trivial information about the Riemannian volume. The most fundamental result of this type is Gromov's lower bound of the minimal volume in terms of the simplicial volume [Gromov1982, Section 0.5][Besson&Courtois&Gallot1991]:
Theorem (Simplicial volume and minimal volume) 3.1.
For all oriented closed connected smooth  -manifolds
-manifolds  we have
we have
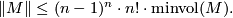
The minimal volume [Gromov1982] of a complete smooth manifold  is defined as
is defined as
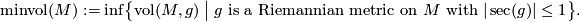
Conversely, in the presence of negative curvature, the simplicial volume is bounded from below by the Riemannian volume [Gromov1982][Thurston1978, Theorem 6.2][Inoue&Yano1982]:
Theorem (Simplicial volume and negative sectional curvature) 3.2.
- The simplicial volume of oriented closed connected Riemannian manifolds of negative sectional curvature is non-zero. More precisely: For every
Tex syntax error
there is a constant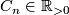 such that the following holds: If
such that the following holds: If  is an oriented closed connected Riemannian
is an oriented closed connected Riemannian  -manifold whose sectional curvature is bounded from above by
-manifold whose sectional curvature is bounded from above by 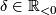 , then
, then
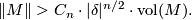
- Let
 be an oriented closed connected hyperbolic
be an oriented closed connected hyperbolic  -manifold. Then
-manifold. Then 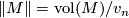 , where
, where 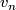 is the supremal volume of all geodesic
is the supremal volume of all geodesic  -simplices in hyperbolic
-simplices in hyperbolic  -space (indeed,
-space (indeed, 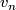 is finite [Thurston1978, Proposition 6.1.4]).
is finite [Thurston1978, Proposition 6.1.4]).
It is well known that 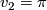 [Thurston1978, p. 6.3], and hence, for any oriented closed connected surface
[Thurston1978, p. 6.3], and hence, for any oriented closed connected surface 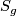 of genus
of genus 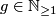 we have
we have 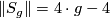 .
.
More generally, there are non-vanishing results for certain manifolds with negatively curved fundamental group.
2 Simplicial volume and bounded cohomology
A more algebraic approach to the simplicial volume is based on the following observation [Gromov1982, p. 17][Benedetti&Petronio1992, F.2.2] (see below for an explanation of the notation):
Proposition (Duality principle) 3.3.
LetTex syntax errorbe a topological space, let
Tex syntax error, and let
Tex syntax error. Then
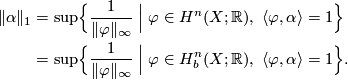
Corollary 3.4.
Let be an oriented closed connected
be an oriented closed connected  -manifold. Then, where
-manifold. Then, where Tex syntax errordenotes the cohomology class dual to the real fundamental class of
 :
:
Tex syntax error
For the sake of completeness, we review the definition of bounded cohomology of topological spaces:
Definition (Bounded cohomology) 3.5.
LetTex syntax errorbe a topological space, and let
Tex syntax error.
- If
Tex syntax error
is a cochain, then we writeIfTex syntax error
Tex syntax error
, thenTex syntax error
is a bounded cochain.
- We write
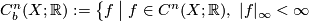 for the subspace of bounded cochains. Notice that
for the subspace of bounded cochains. Notice that Tex syntax error
is a subcomplex of the singular cochain complex, called the bounded cochain complex ofTex syntax error
. - The cohomology
Tex syntax error
of is the bounded cohomology of
is the bounded cohomology of Tex syntax error
. - The norm
Tex syntax error
on the bounded cochain complex induces a semi-norm on bounded cohomology: IfTex syntax error
, then
Tex syntax error
- The inclusion
Tex syntax error
induces a homomorphismTex syntax error
, the comparison map.
Bounded cohomology was originally introduced by Trauber. Gromov further developed bounded cohomology and studied its relation with the (Riemannian) volume of manifolds [Gromov1982]. A more algebraic approach to bounded cohomology was subsequently developed by Brooks [Brooks1978], Ivanov [Ivanov1985], Noskov [Noskov1990], Monod [Monod2001][Monod2006], and Bühler [Bühler2008].
In the context of simplicial volume, bounded cohomology contributed to establish vanishing results in the presence of amenable fundamental groups, non-vanishing results in the presence of certain types of negative curvature, and inheritance properties with respect to products, connected sums, shared Riemannian coverings.
4 References
- [Benedetti&Petronio1992] R. Benedetti and C. Petronio, Lectures on hyperbolic geometry, Springer-Verlag, Berlin, 1992. MR1219310 (94e:57015) Zbl 0768.51018
- [Besson&Courtois&Gallot1991] G. Besson, G. Courtois and S. Gallot, Volume et entropie minimale des espaces localement symétriques, Invent. Math. 103 (1991), no.2, 417–445. MR1085114 (92d:58027) Zbl 0723.53029
- [Brooks1978] R. Brooks, Some remarks on bounded cohomology, in Riemann surfaces and related topics: Proceedings of the 1978 Stonybrook Conference, Ann. of Math. Stud., 97 (1978), 53–63. MR624804 (83a:57038) Zbl 0457.55002
- [Bühler2008] T. Bühler, A derived functor approach to bounded cohomology, C. R. Math. Acad. Sci. Paris 346 (2008), no.11-12, 615–618. MR2423264 (2009f:18013) Zbl 1148.18007
- [Gromov1982] M. Gromov, Volume and bounded cohomology, Inst. Hautes Études Sci. Publ. Math. (1982), no.56, 5–99 (1983). MR686042 (84h:53053) Zbl 0516.53046
- [Gromov1999] M. Gromov, Metric structures for Riemannian and non-Riemannian spaces, Birkhäuser Boston Inc., Boston, MA, 1999. MR1699320 (2000d:53065) Zbl 1113.53001
- [Inoue&Yano1982] H. Inoue and K. Yano, The Gromov invariant of negatively curved manifolds, Topology 21 (1982), no.1, 83–89. MR630882 (82k:53091) Zbl 0469.53038
- [Ivanov1985] N. V. Ivanov, Foundations of the theory of bounded cohomology, Zap. Nauchn. Sem. Leningrad. Otdel. Mat. Inst. Steklov. (LOMI) 143 (1985), 69–109, 177. MR806562 (87b:53070) Zbl 0612.55006
- [Monod2001] N. Monod, Continuous bounded cohomology of locally compact groups, Springer-Verlag, Berlin, 2001. MR1840942 (2002h:46121) Zbl 0967.22006
- [Monod2006] N. Monod, An invitation to bounded cohomology, International Congress of Mathematicians. Vol. II, Eur. Math. Soc., Zürich, (2006), 1183–1211. MR2275641 (2008e:22011) Zbl 1127.55002
- [Munkholm1980] H. J. Munkholm, Simplices of maximal volume in hyperbolic space, Gromov's norm, and Gromov's proof of Mostow's rigidity theorem (following Thurston), 788 (1980), 109–124. MR585656 (81k:53046) Zbl 0434.57017
- [Noskov1990] G. A. Noskov, Bounded cohomology of discrete groups with coefficients, Algebra i Analiz 2 (1990), no.5, 146–164. MR1086449 (92b:57005) Zbl 0729.55005
- [Thurston1978] W. P. Thurston, The Geometry and Topology of 3-Manifolds. Lecture notes, Princeton, 1978.
|
This page has not been refereed. The information given here might be incomplete or provisional. |
 .
Then the simplicial volume (also called Gromov norm) of
.
Then the simplicial volume (also called Gromov norm) of  is defined as
is defined as
![\displaystyle \|M\| := \bigl\| [M] \bigr\|_1 = \inf \bigl\{ |c|_1 \bigm| \text{$c \in C_n(M;\mathbb{R})$ is a fundamental cycle of $M$} \bigr\} \in \mathbb{R}_{\geq 0},](/images/math/c/2/2/c22511eadabaaaa5caa7565812d6977a.png)
where ![[M] \in H_n(M;\mathbb{R})](/images/math/7/d/7/7d74a20a6efc50970d884cfa1c1e5861.png) is the fundamental class of
is the fundamental class of  with real coefficients.
with real coefficients.
- Here,
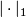 denotes the
denotes the  -norm on the singular chain complex
-norm on the singular chain complex 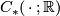 with real coefficients induced from the (unordered) basis given by all singular simplices, i.e.: for a topological space
with real coefficients induced from the (unordered) basis given by all singular simplices, i.e.: for a topological space Tex syntax error
and a chain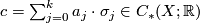 (in reduced form), the
(in reduced form), the  -norm of
-norm of  is given by
is given by
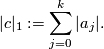
- Moreover,
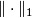 denotes the
denotes the  -semi-norm on singular homology
-semi-norm on singular homology 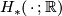 with real coefficients, which is induced by
with real coefficients, which is induced by 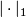 . More explicitly, if
. More explicitly, if Tex syntax error
is a topological space and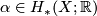 , then
, then
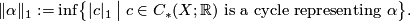
Convention 1.2. In the following, if not explicitly stated otherwise, all manifolds are topological manifolds and are of non-zero dimension.
2 Functoriality and elementary examples
The  -semi-norm is functorial in the following sense [Gromov1999]:
-semi-norm is functorial in the following sense [Gromov1999]:
Proposition (Functoriality of the  -semi-norm) 2.1.
If
-semi-norm) 2.1.
If 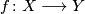 is a continuous map of topological spaces and
is a continuous map of topological spaces and 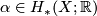 , then
, then
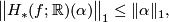
as can be seen by inspecting the definition of 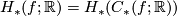 and of
and of 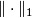 .
.
Corollary 2.2.
- Let
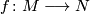 be a map of oriented closed connected manifolds of the same dimension. Then
be a map of oriented closed connected manifolds of the same dimension. Then
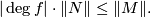
- Because homotopy equivalences of oriented closed connected manifolds have degree
 or
or  , it follows that the simplicial volume indeed is a homotopy invariant of oriented closed connected manifolds.
, it follows that the simplicial volume indeed is a homotopy invariant of oriented closed connected manifolds.
Hence, all oriented closed connected manifolds admitting a self-map of non-trivial degree (i.e., not equal to  ,
,  , or
, or  ) have vanishing simplicial volume; for instance, the simplicial volume of all
) have vanishing simplicial volume; for instance, the simplicial volume of all
- spheres
- tori
- (odd-dimensional) real projective spaces
- complex projective spaces
is zero.
3 "Computing" simplicial volume
In most cases, trying to compute the simplicial volume by inspecting the definition proves to be futile;
the two main sources for non-trivial estimates and inheritance properties of the simplicial volume are:
- Geometric: The connection between simplicial volume and Riemannian geometry (see below).
- Algebraic: The connection between simplicial volume and bounded cohomology (see below).
1 Simplicial volume and Riemannian geometry
A fascinating aspect of the simplicial volume is that it is a homotopy invariant encoding non-trivial information about the Riemannian volume. The most fundamental result of this type is Gromov's lower bound of the minimal volume in terms of the simplicial volume [Gromov1982, Section 0.5][Besson&Courtois&Gallot1991]:
Theorem (Simplicial volume and minimal volume) 3.1.
For all oriented closed connected smooth  -manifolds
-manifolds  we have
we have
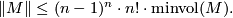
The minimal volume [Gromov1982] of a complete smooth manifold  is defined as
is defined as
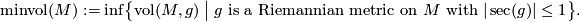
Conversely, in the presence of negative curvature, the simplicial volume is bounded from below by the Riemannian volume [Gromov1982][Thurston1978, Theorem 6.2][Inoue&Yano1982]:
Theorem (Simplicial volume and negative sectional curvature) 3.2.
- The simplicial volume of oriented closed connected Riemannian manifolds of negative sectional curvature is non-zero. More precisely: For every
Tex syntax error
there is a constant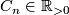 such that the following holds: If
such that the following holds: If  is an oriented closed connected Riemannian
is an oriented closed connected Riemannian  -manifold whose sectional curvature is bounded from above by
-manifold whose sectional curvature is bounded from above by 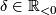 , then
, then
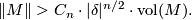
- Let
 be an oriented closed connected hyperbolic
be an oriented closed connected hyperbolic  -manifold. Then
-manifold. Then 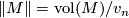 , where
, where 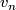 is the supremal volume of all geodesic
is the supremal volume of all geodesic  -simplices in hyperbolic
-simplices in hyperbolic  -space (indeed,
-space (indeed, 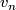 is finite [Thurston1978, Proposition 6.1.4]).
is finite [Thurston1978, Proposition 6.1.4]).
It is well known that 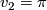 [Thurston1978, p. 6.3], and hence, for any oriented closed connected surface
[Thurston1978, p. 6.3], and hence, for any oriented closed connected surface 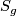 of genus
of genus 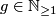 we have
we have 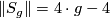 .
.
More generally, there are non-vanishing results for certain manifolds with negatively curved fundamental group.
2 Simplicial volume and bounded cohomology
A more algebraic approach to the simplicial volume is based on the following observation [Gromov1982, p. 17][Benedetti&Petronio1992, F.2.2] (see below for an explanation of the notation):
Proposition (Duality principle) 3.3.
LetTex syntax errorbe a topological space, let
Tex syntax error, and let
Tex syntax error. Then
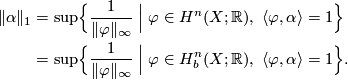
Corollary 3.4.
Let be an oriented closed connected
be an oriented closed connected  -manifold. Then, where
-manifold. Then, where Tex syntax errordenotes the cohomology class dual to the real fundamental class of
 :
:
Tex syntax error
For the sake of completeness, we review the definition of bounded cohomology of topological spaces:
Definition (Bounded cohomology) 3.5.
LetTex syntax errorbe a topological space, and let
Tex syntax error.
- If
Tex syntax error
is a cochain, then we writeIfTex syntax error
Tex syntax error
, thenTex syntax error
is a bounded cochain.
- We write
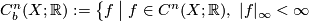 for the subspace of bounded cochains. Notice that
for the subspace of bounded cochains. Notice that Tex syntax error
is a subcomplex of the singular cochain complex, called the bounded cochain complex ofTex syntax error
. - The cohomology
Tex syntax error
of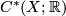 is the bounded cohomology of
is the bounded cohomology of Tex syntax error
. - The norm
Tex syntax error
on the bounded cochain complex induces a semi-norm on bounded cohomology: IfTex syntax error
, then
Tex syntax error
- The inclusion
Tex syntax error
induces a homomorphismTex syntax error
, the comparison map.
Bounded cohomology was originally introduced by Trauber. Gromov further developed bounded cohomology and studied its relation with the (Riemannian) volume of manifolds [Gromov1982]. A more algebraic approach to bounded cohomology was subsequently developed by Brooks [Brooks1978], Ivanov [Ivanov1985], Noskov [Noskov1990], Monod [Monod2001][Monod2006], and Bühler [Bühler2008].
In the context of simplicial volume, bounded cohomology contributed to establish vanishing results in the presence of amenable fundamental groups, non-vanishing results in the presence of certain types of negative curvature, and inheritance properties with respect to products, connected sums, shared Riemannian coverings.
4 References
- [Benedetti&Petronio1992] R. Benedetti and C. Petronio, Lectures on hyperbolic geometry, Springer-Verlag, Berlin, 1992. MR1219310 (94e:57015) Zbl 0768.51018
- [Besson&Courtois&Gallot1991] G. Besson, G. Courtois and S. Gallot, Volume et entropie minimale des espaces localement symétriques, Invent. Math. 103 (1991), no.2, 417–445. MR1085114 (92d:58027) Zbl 0723.53029
- [Brooks1978] R. Brooks, Some remarks on bounded cohomology, in Riemann surfaces and related topics: Proceedings of the 1978 Stonybrook Conference, Ann. of Math. Stud., 97 (1978), 53–63. MR624804 (83a:57038) Zbl 0457.55002
- [Bühler2008] T. Bühler, A derived functor approach to bounded cohomology, C. R. Math. Acad. Sci. Paris 346 (2008), no.11-12, 615–618. MR2423264 (2009f:18013) Zbl 1148.18007
- [Gromov1982] M. Gromov, Volume and bounded cohomology, Inst. Hautes Études Sci. Publ. Math. (1982), no.56, 5–99 (1983). MR686042 (84h:53053) Zbl 0516.53046
- [Gromov1999] M. Gromov, Metric structures for Riemannian and non-Riemannian spaces, Birkhäuser Boston Inc., Boston, MA, 1999. MR1699320 (2000d:53065) Zbl 1113.53001
- [Inoue&Yano1982] H. Inoue and K. Yano, The Gromov invariant of negatively curved manifolds, Topology 21 (1982), no.1, 83–89. MR630882 (82k:53091) Zbl 0469.53038
- [Ivanov1985] N. V. Ivanov, Foundations of the theory of bounded cohomology, Zap. Nauchn. Sem. Leningrad. Otdel. Mat. Inst. Steklov. (LOMI) 143 (1985), 69–109, 177. MR806562 (87b:53070) Zbl 0612.55006
- [Monod2001] N. Monod, Continuous bounded cohomology of locally compact groups, Springer-Verlag, Berlin, 2001. MR1840942 (2002h:46121) Zbl 0967.22006
- [Monod2006] N. Monod, An invitation to bounded cohomology, International Congress of Mathematicians. Vol. II, Eur. Math. Soc., Zürich, (2006), 1183–1211. MR2275641 (2008e:22011) Zbl 1127.55002
- [Munkholm1980] H. J. Munkholm, Simplices of maximal volume in hyperbolic space, Gromov's norm, and Gromov's proof of Mostow's rigidity theorem (following Thurston), 788 (1980), 109–124. MR585656 (81k:53046) Zbl 0434.57017
- [Noskov1990] G. A. Noskov, Bounded cohomology of discrete groups with coefficients, Algebra i Analiz 2 (1990), no.5, 146–164. MR1086449 (92b:57005) Zbl 0729.55005
- [Thurston1978] W. P. Thurston, The Geometry and Topology of 3-Manifolds. Lecture notes, Princeton, 1978.
|
This page has not been refereed. The information given here might be incomplete or provisional. |
 .
Then the simplicial volume (also called Gromov norm) of
.
Then the simplicial volume (also called Gromov norm) of  is defined as
is defined as
![\displaystyle \|M\| := \bigl\| [M] \bigr\|_1 = \inf \bigl\{ |c|_1 \bigm| \text{$c \in C_n(M;\mathbb{R})$ is a fundamental cycle of $M$} \bigr\} \in \mathbb{R}_{\geq 0},](/images/math/c/2/2/c22511eadabaaaa5caa7565812d6977a.png)
where ![[M] \in H_n(M;\mathbb{R})](/images/math/7/d/7/7d74a20a6efc50970d884cfa1c1e5861.png) is the fundamental class of
is the fundamental class of  with real coefficients.
with real coefficients.
- Here,
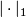 denotes the
denotes the  -norm on the singular chain complex
-norm on the singular chain complex 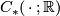 with real coefficients induced from the (unordered) basis given by all singular simplices, i.e.: for a topological space
with real coefficients induced from the (unordered) basis given by all singular simplices, i.e.: for a topological space Tex syntax error
and a chain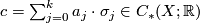 (in reduced form), the
(in reduced form), the  -norm of
-norm of  is given by
is given by
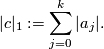
- Moreover,
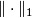 denotes the
denotes the  -semi-norm on singular homology
-semi-norm on singular homology 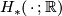 with real coefficients, which is induced by
with real coefficients, which is induced by  . More explicitly, if
. More explicitly, if Tex syntax error
is a topological space and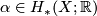 , then
, then
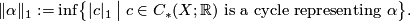
Convention 1.2. In the following, if not explicitly stated otherwise, all manifolds are topological manifolds and are of non-zero dimension.
2 Functoriality and elementary examples
The  -semi-norm is functorial in the following sense [Gromov1999]:
-semi-norm is functorial in the following sense [Gromov1999]:
Proposition (Functoriality of the  -semi-norm) 2.1.
If
-semi-norm) 2.1.
If 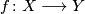 is a continuous map of topological spaces and
is a continuous map of topological spaces and 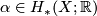 , then
, then
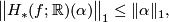
as can be seen by inspecting the definition of 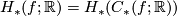 and of
and of 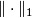 .
.
Corollary 2.2.
- Let
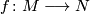 be a map of oriented closed connected manifolds of the same dimension. Then
be a map of oriented closed connected manifolds of the same dimension. Then
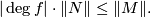
- Because homotopy equivalences of oriented closed connected manifolds have degree
 or
or  , it follows that the simplicial volume indeed is a homotopy invariant of oriented closed connected manifolds.
, it follows that the simplicial volume indeed is a homotopy invariant of oriented closed connected manifolds.
Hence, all oriented closed connected manifolds admitting a self-map of non-trivial degree (i.e., not equal to  ,
,  , or
, or  ) have vanishing simplicial volume; for instance, the simplicial volume of all
) have vanishing simplicial volume; for instance, the simplicial volume of all
- spheres
- tori
- (odd-dimensional) real projective spaces
- complex projective spaces
is zero.
3 "Computing" simplicial volume
In most cases, trying to compute the simplicial volume by inspecting the definition proves to be futile;
the two main sources for non-trivial estimates and inheritance properties of the simplicial volume are:
- Geometric: The connection between simplicial volume and Riemannian geometry (see below).
- Algebraic: The connection between simplicial volume and bounded cohomology (see below).
1 Simplicial volume and Riemannian geometry
A fascinating aspect of the simplicial volume is that it is a homotopy invariant encoding non-trivial information about the Riemannian volume. The most fundamental result of this type is Gromov's lower bound of the minimal volume in terms of the simplicial volume [Gromov1982, Section 0.5][Besson&Courtois&Gallot1991]:
Theorem (Simplicial volume and minimal volume) 3.1.
For all oriented closed connected smooth  -manifolds
-manifolds  we have
we have
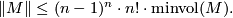
The minimal volume [Gromov1982] of a complete smooth manifold  is defined as
is defined as
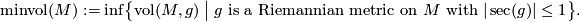
Conversely, in the presence of negative curvature, the simplicial volume is bounded from below by the Riemannian volume [Gromov1982][Thurston1978, Theorem 6.2][Inoue&Yano1982]:
Theorem (Simplicial volume and negative sectional curvature) 3.2.
- The simplicial volume of oriented closed connected Riemannian manifolds of negative sectional curvature is non-zero. More precisely: For every
Tex syntax error
there is a constant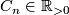 such that the following holds: If
such that the following holds: If  is an oriented closed connected Riemannian
is an oriented closed connected Riemannian  -manifold whose sectional curvature is bounded from above by
-manifold whose sectional curvature is bounded from above by 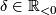 , then
, then
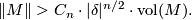
- Let
 be an oriented closed connected hyperbolic
be an oriented closed connected hyperbolic  -manifold. Then
-manifold. Then 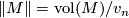 , where
, where 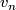 is the supremal volume of all geodesic
is the supremal volume of all geodesic  -simplices in hyperbolic
-simplices in hyperbolic  -space (indeed,
-space (indeed, 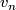 is finite [Thurston1978, Proposition 6.1.4]).
is finite [Thurston1978, Proposition 6.1.4]).
It is well known that 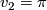 [Thurston1978, p. 6.3], and hence, for any oriented closed connected surface
[Thurston1978, p. 6.3], and hence, for any oriented closed connected surface 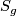 of genus
of genus 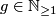 we have
we have 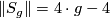 .
.
More generally, there are non-vanishing results for certain manifolds with negatively curved fundamental group.
2 Simplicial volume and bounded cohomology
A more algebraic approach to the simplicial volume is based on the following observation [Gromov1982, p. 17][Benedetti&Petronio1992, F.2.2] (see below for an explanation of the notation):
Proposition (Duality principle) 3.3.
LetTex syntax errorbe a topological space, let
Tex syntax error, and let
Tex syntax error. Then
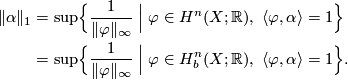
Corollary 3.4.
Let be an oriented closed connected
be an oriented closed connected  -manifold. Then, where
-manifold. Then, where Tex syntax errordenotes the cohomology class dual to the real fundamental class of
 :
:
Tex syntax error
For the sake of completeness, we review the definition of bounded cohomology of topological spaces:
Definition (Bounded cohomology) 3.5.
LetTex syntax errorbe a topological space, and let
Tex syntax error.
- If
Tex syntax error
is a cochain, then we writeIfTex syntax error
Tex syntax error
, thenTex syntax error
is a bounded cochain.
- We write
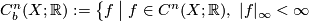 for the subspace of bounded cochains. Notice that
for the subspace of bounded cochains. Notice that Tex syntax error
is a subcomplex of the singular cochain complex, called the bounded cochain complex ofTex syntax error
. - The cohomology
Tex syntax error
of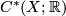 is the bounded cohomology of
is the bounded cohomology of Tex syntax error
. - The norm
Tex syntax error
on the bounded cochain complex induces a semi-norm on bounded cohomology: IfTex syntax error
, then
Tex syntax error
- The inclusion
Tex syntax error
induces a homomorphismTex syntax error
, the comparison map.
Bounded cohomology was originally introduced by Trauber. Gromov further developed bounded cohomology and studied its relation with the (Riemannian) volume of manifolds [Gromov1982]. A more algebraic approach to bounded cohomology was subsequently developed by Brooks [Brooks1978], Ivanov [Ivanov1985], Noskov [Noskov1990], Monod [Monod2001][Monod2006], and Bühler [Bühler2008].
In the context of simplicial volume, bounded cohomology contributed to establish vanishing results in the presence of amenable fundamental groups, non-vanishing results in the presence of certain types of negative curvature, and inheritance properties with respect to products, connected sums, shared Riemannian coverings.
4 References
- [Benedetti&Petronio1992] R. Benedetti and C. Petronio, Lectures on hyperbolic geometry, Springer-Verlag, Berlin, 1992. MR1219310 (94e:57015) Zbl 0768.51018
- [Besson&Courtois&Gallot1991] G. Besson, G. Courtois and S. Gallot, Volume et entropie minimale des espaces localement symétriques, Invent. Math. 103 (1991), no.2, 417–445. MR1085114 (92d:58027) Zbl 0723.53029
- [Brooks1978] R. Brooks, Some remarks on bounded cohomology, in Riemann surfaces and related topics: Proceedings of the 1978 Stonybrook Conference, Ann. of Math. Stud., 97 (1978), 53–63. MR624804 (83a:57038) Zbl 0457.55002
- [Bühler2008] T. Bühler, A derived functor approach to bounded cohomology, C. R. Math. Acad. Sci. Paris 346 (2008), no.11-12, 615–618. MR2423264 (2009f:18013) Zbl 1148.18007
- [Gromov1982] M. Gromov, Volume and bounded cohomology, Inst. Hautes Études Sci. Publ. Math. (1982), no.56, 5–99 (1983). MR686042 (84h:53053) Zbl 0516.53046
- [Gromov1999] M. Gromov, Metric structures for Riemannian and non-Riemannian spaces, Birkhäuser Boston Inc., Boston, MA, 1999. MR1699320 (2000d:53065) Zbl 1113.53001
- [Inoue&Yano1982] H. Inoue and K. Yano, The Gromov invariant of negatively curved manifolds, Topology 21 (1982), no.1, 83–89. MR630882 (82k:53091) Zbl 0469.53038
- [Ivanov1985] N. V. Ivanov, Foundations of the theory of bounded cohomology, Zap. Nauchn. Sem. Leningrad. Otdel. Mat. Inst. Steklov. (LOMI) 143 (1985), 69–109, 177. MR806562 (87b:53070) Zbl 0612.55006
- [Monod2001] N. Monod, Continuous bounded cohomology of locally compact groups, Springer-Verlag, Berlin, 2001. MR1840942 (2002h:46121) Zbl 0967.22006
- [Monod2006] N. Monod, An invitation to bounded cohomology, International Congress of Mathematicians. Vol. II, Eur. Math. Soc., Zürich, (2006), 1183–1211. MR2275641 (2008e:22011) Zbl 1127.55002
- [Munkholm1980] H. J. Munkholm, Simplices of maximal volume in hyperbolic space, Gromov's norm, and Gromov's proof of Mostow's rigidity theorem (following Thurston), 788 (1980), 109–124. MR585656 (81k:53046) Zbl 0434.57017
- [Noskov1990] G. A. Noskov, Bounded cohomology of discrete groups with coefficients, Algebra i Analiz 2 (1990), no.5, 146–164. MR1086449 (92b:57005) Zbl 0729.55005
- [Thurston1978] W. P. Thurston, The Geometry and Topology of 3-Manifolds. Lecture notes, Princeton, 1978.
|
This page has not been refereed. The information given here might be incomplete or provisional. |
- If $f \in C^n(X;\mathbb{R})$ is a cochain, then we write $$ |f|_\infty := \sup_{\sigma \in \mathop{\mathrm{map}} (\Delta^n,X)} |f(\sigma)| \in \mathbb{R}_{\geq 0} \cup \{\infty\}. $$ If $|f|_\infty < \infty$, then $f$ is a '''bounded cochain'''.
 .
Then the simplicial volume (also called Gromov norm) of
.
Then the simplicial volume (also called Gromov norm) of  is defined as
is defined as
![\displaystyle \|M\| := \bigl\| [M] \bigr\|_1 = \inf \bigl\{ |c|_1 \bigm| \text{$c \in C_n(M;\mathbb{R})$ is a fundamental cycle of $M$} \bigr\} \in \mathbb{R}_{\geq 0},](/images/math/c/2/2/c22511eadabaaaa5caa7565812d6977a.png)
where ![[M] \in H_n(M;\mathbb{R})](/images/math/7/d/7/7d74a20a6efc50970d884cfa1c1e5861.png) is the fundamental class of
is the fundamental class of  with real coefficients.
with real coefficients.
- Here,
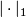 denotes the
denotes the  -norm on the singular chain complex
-norm on the singular chain complex 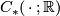 with real coefficients induced from the (unordered) basis given by all singular simplices, i.e.: for a topological space
with real coefficients induced from the (unordered) basis given by all singular simplices, i.e.: for a topological space Tex syntax error
and a chain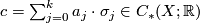 (in reduced form), the
(in reduced form), the  -norm of
-norm of  is given by
is given by
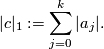
- Moreover,
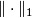 denotes the
denotes the  -semi-norm on singular homology
-semi-norm on singular homology 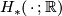 with real coefficients, which is induced by
with real coefficients, which is induced by 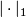 . More explicitly, if
. More explicitly, if Tex syntax error
is a topological space and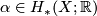 , then
, then