Simplicial volume
|
An earlier version of this page was published in the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 09:51, 1 April 2011 and the changes since publication. |
|
The user responsible for this page is Clara Löh. No other user may edit this page at present. |
Contents |
1 Definition and history
Simplicial volume is a homotopy invariant of oriented closed connected manifolds that was introduced by Gromov in his proof of Mostow rigidity [Munkholm1980][Gromov1982]. Intuitively, simplicial volume measures how difficult it is to describe the manifold in question in terms of simplices (with real coefficients):
Definition (Simplicial volume) 1.1.
Let  be an oriented closed connected manifold of dimension
be an oriented closed connected manifold of dimension  .
Then the simplicial volume of
.
Then the simplicial volume of  (also called the Gromov norm of
(also called the Gromov norm of  ) is defined as
) is defined as
![\displaystyle \|M\| := \bigl\| [M] \bigr\|_1 = \inf \bigl\{ |c|_1 \bigm| \text{$c \in C_n(M;\mathbb{R})$ is a fundamental cycle of $M$} \bigr\} \in \mathbb{R}_{\geq 0},](/images/math/c/2/2/c22511eadabaaaa5caa7565812d6977a.png)
where ![[M] \in H_n(M;\mathbb{R})](/images/math/7/d/7/7d74a20a6efc50970d884cfa1c1e5861.png) is the fundamental class of
is the fundamental class of  with real coefficients.
with real coefficients.
- Here,
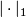 denotes the
denotes the  -norm on the singular chain complex
-norm on the singular chain complex 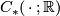 with real coefficients induced from the (unordered) basis given by all singular simplices, i.e.: for a topological space
with real coefficients induced from the (unordered) basis given by all singular simplices, i.e.: for a topological space  and a chain
and a chain 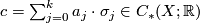 (in reduced form), the
(in reduced form), the  -norm of
-norm of  is given by
is given by
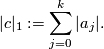
- Moreover,
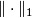 denotes the
denotes the  -semi-norm on singular homology
-semi-norm on singular homology 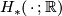 with real coefficients, which is induced by
with real coefficients, which is induced by 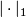 . More explicitly, if
. More explicitly, if  is a topological space and
is a topological space and 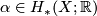 , then
, then
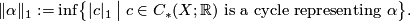
Convention 1.2. In the following, if not explicitly stated otherwise, all manifolds are topological manifolds and are of non-zero dimension.
2 Functoriality and elementary examples
The  -semi-norm is functorial in the following sense [Gromov1999, Section 5.34]:
-semi-norm is functorial in the following sense [Gromov1999, Section 5.34]:
Proposition (Functoriality of the  -semi-norm) 2.1.
If
-semi-norm) 2.1.
If 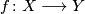 is a continuous map of topological spaces and
is a continuous map of topological spaces and 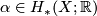 , then
, then
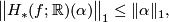
as can be seen by inspecting the definition of 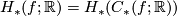 and of
and of 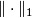 .
.
Corollary 2.2.
- Let
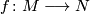 be a map of oriented closed connected manifolds of the same dimension. Then
be a map of oriented closed connected manifolds of the same dimension. Then
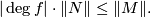
- Because homotopy equivalences of oriented closed connected manifolds have degree
 or
or  , it follows that simplicial volume indeed is a homotopy invariant of oriented closed connected manifolds.
, it follows that simplicial volume indeed is a homotopy invariant of oriented closed connected manifolds.
Hence, all oriented closed connected manifolds admitting a self-map of non-trivial degree (i.e., not equal to  ,
,  , or
, or  ) have vanishing simplicial volume; for instance, the simplicial volume of all
) have vanishing simplicial volume; for instance, the simplicial volume of all
- spheres
- tori
- (odd-dimensional) real projective spaces
- complex projective spaces
is zero. Similarly, any oriented closed connected smooth manifold that admits a non-trivial smooth  -action has vanishing simplicial volume [Yano1982].
-action has vanishing simplicial volume [Yano1982].
3 "Computing" simplicial volume
In most cases, trying to compute simplicial volume by inspecting the definition proves to be futile; the two main sources for non-trivial estimates and inheritance properties of simplicial volume are:
- Geometric approach: The connection between simplicial volume and Riemannian geometry (see below).
- Algebraic approach: The connection between simplicial volume and bounded cohomology (see below).
3.1 Simplicial volume and Riemannian geometry
A fascinating aspect of simplicial volume is that it is a homotopy invariant encoding non-trivial information about the Riemannian volume. The most fundamental result of this type is Gromov's Main Inequality [Gromov1982, Section 0.5] and the resulting lower bound of the minimal volume in terms of the simplicial volume [Gromov1982, Section 0.5] (the improved upper bound is due to Besson, Courtois, and Gallot [Besson&Courtois&Gallot1991, Théorème D]):
Theorem (Main Inequality) 3.1.
For all oriented closed connected Riemannian  -manifolds
-manifolds  whose Ricci curvature is bounded from below by
whose Ricci curvature is bounded from below by 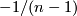 we have
we have
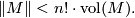
Theorem (Simplicial volume and minimal volume) 3.2.
For all oriented closed connected smooth  -manifolds
-manifolds  we have
we have
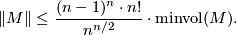
The minimal volume [Gromov1982] of a complete smooth manifold  is defined as
is defined as
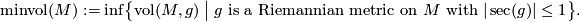
Conversely, in the presence of negative curvature, the simplicial volume is bounded from below by the Riemannian volume [Gromov1982, Section 0.3][Thurston1978, Theorem 6.2][Inoue&Yano1982]:
Theorem (Simplicial volume and negative sectional curvature) 3.3.
- The simplicial volume of oriented closed connected Riemannian manifolds of negative sectional curvature is non-zero. More precisely: For every
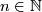 there is a constant
there is a constant 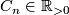 such that the following holds: If
such that the following holds: If  is an oriented closed connected Riemannian
is an oriented closed connected Riemannian  -manifold whose sectional curvature is bounded from above by
-manifold whose sectional curvature is bounded from above by 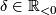 , then
, then
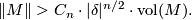
- Let
 be an oriented closed connected hyperbolic
be an oriented closed connected hyperbolic  -manifold. Then
-manifold. Then 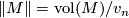 , where
, where 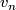 is the supremal volume of all geodesic
is the supremal volume of all geodesic  -simplices in hyperbolic
-simplices in hyperbolic  -space (indeed,
-space (indeed, 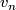 is finite [Thurston1978, Proposition 6.1.4]).
is finite [Thurston1978, Proposition 6.1.4]).
The proof of the lower bound 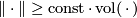 consists of "straightening" fundamental cycles to cycles consisting only of singular simplices whose lifts to the Riemannian universal covering are geodesic.
consists of "straightening" fundamental cycles to cycles consisting only of singular simplices whose lifts to the Riemannian universal covering are geodesic.
It is well known that 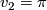 [Thurston1978, p. 6.3], and hence, for any oriented closed connected surface
[Thurston1978, p. 6.3], and hence, for any oriented closed connected surface 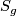 of genus
of genus 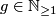 we have
we have 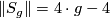 .
.
Generalisations of Theorem 3.3 are:
- The proportionality principle for simplicial volume (Theorem 4.4);
- the non-vanishing of the simplicial volume of oriented closed connected locally symmetric spaces of non-compact type [Lafont&Schmidt2006] (which is obtained by a combination of a generalised straightening using estimates of Connell and Farb [Connell&Farb2003] and the proportionality principle);
- non-vanishing results for certain manifolds with negatively curved fundamental group (see below);
- the construction of (aspherical) oriented closed connected manifolds of non-zero simplicial volume via (relative) hyperbolisation techniques [Belegradek2006].
3.2 Simplicial volume and bounded cohomology
A more algebraic approach to simplicial volume is based on the following observation [Gromov1982, p. 17][Benedetti&Petronio1992, F.2.2] (see below for an explanation of the notation):
Proposition (Duality principle) 3.4.
Let  be a topological space, let
be a topological space, let 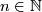 , and let
, and let 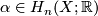 . Then
. Then
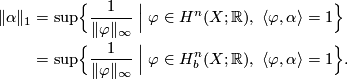
Corollary 3.5.
Let  be an oriented closed connected
be an oriented closed connected  -manifold. Then (where
-manifold. Then (where ![[M]^* \in H^n(M;\mathbb{R})](/images/math/3/9/8/3989b8305e26d91bef3331c942cad1d4.png) denotes the cohomology class dual to the real fundamental class of
denotes the cohomology class dual to the real fundamental class of  ):
):
![\displaystyle \begin{aligned} \| M \| & = \frac{1}{\bigl\| [M]^* \bigr\|_\infty}\\ & = \sup \Bigl\{ \frac{1}{\|\varphi\|_\infty} \Bigm| \varphi \in H_b^n(M;\mathbb{R}),~c_M(\varphi) = [M]^* \Bigr\}. \end{aligned}](/images/math/9/b/e/9be40a109f4996a49bb99015b26467ff.png)
For the sake of completeness, we review the definition of bounded cohomology of topological spaces:
Definition (Bounded cohomology) 3.6.
Let  be a topological space, and let
be a topological space, and let 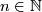 .
.
- If
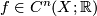 is a cochain, then we write
is a cochain, then we write
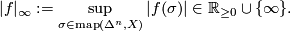
If
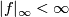 , then
, then  is a bounded cochain.
is a bounded cochain.
- We write
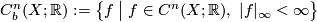 for the subspace of bounded cochains. Notice that
for the subspace of bounded cochains. Notice that 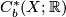 is a subcomplex of the singular cochain complex, called the bounded cochain complex of
is a subcomplex of the singular cochain complex, called the bounded cochain complex of  .
.
- The cohomology
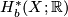 of
of 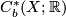 is the bounded cohomology of
is the bounded cohomology of  . (It is not difficult to see that every continuous map induces a homomorphism on the level of bounded cohomology; turning
. (It is not difficult to see that every continuous map induces a homomorphism on the level of bounded cohomology; turning 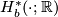 into a contravariant functor).
into a contravariant functor).
- The norm
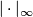 on the bounded cochain complex induces a semi-norm on bounded cohomology: If
on the bounded cochain complex induces a semi-norm on bounded cohomology: If 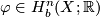 , then
, then
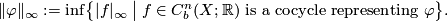
- The natural inclusion
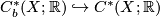 induces a natural homomorphism
induces a natural homomorphism 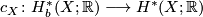 , the comparison map.
, the comparison map.
Bounded cohomology was originally introduced by Trauber. Gromov further developed bounded cohomology and studied its relation with the (Riemannian) volume of manifolds [Gromov1982]. A more algebraic approach to bounded cohomology was subsequently developed by Brooks [Brooks1978], Ivanov [Ivanov1985], Noskov [Noskov1990], Monod [Monod2001][Monod2006], and Bühler [Bühler2008].
In the context of simplicial volume, bounded cohomology contributed to establish vanishing results in the presence of amenable fundamental groups, non-vanishing results in the presence of certain types of negative curvature, and inheritance properties with respect to products, connected sums and shared Riemannian coverings.
4 Inheritance properties
4.1 Finite Coverings
Simplicial volume is multiplicative with respect to finite coverings:
Proposition (Simplicial volume and finite coverings) 4.1.
Let 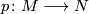 be a covering map of oriented closed connected manifolds, and let
be a covering map of oriented closed connected manifolds, and let  be the (finite!) number of sheets of
be the (finite!) number of sheets of  . Then
. Then
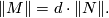
For the proof notice that 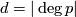 and that
and that 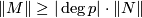 by functoriality (Corollary 2.2); to show the converse inequality
by functoriality (Corollary 2.2); to show the converse inequality 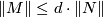 one can use the transfer on singular chains.
one can use the transfer on singular chains.
4.2 Products
Simplicial volume is almost multiplicative with respect to direct products of manifolds [Gromov1982, p. 10][Benedetti&Petronio1992, Theorem F.2.5]:
Theorem (Simplicial volume and products) 4.2.
Let  and
and  be oriented closed connected manifolds. Then
be oriented closed connected manifolds. Then
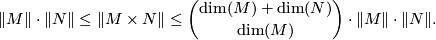
A proof of the right hand estimate can be given by looking at the concrete description of ![[M \times N] = [M] \times [N]](/images/math/b/9/9/b99d62f494a7260873166d93375f120e.png) in terms of the cross-product of singular chains; a proof of the left hand estimate can be obtained by using the duality principle (Corollary 3.5) and the fact that the norm
in terms of the cross-product of singular chains; a proof of the left hand estimate can be obtained by using the duality principle (Corollary 3.5) and the fact that the norm 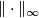 is submultiplicative with respect to the cross-product of (bounded) singular cochains.
is submultiplicative with respect to the cross-product of (bounded) singular cochains.
Notice that simplicial volume in general is not multiplicative: Bucher-Karlsson [Bucher-Karlsson2008, Corollary 2] proved that 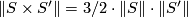 holds for all oriented closed connected surfaces
holds for all oriented closed connected surfaces  ,
, 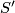 of genus at least
of genus at least  (and
(and 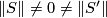 (see above)).
(see above)).
4.3 Connected sums
Simplicial volume is additive with respect to connected sums in the following sense [Gromov1982, p. 10]:
Theorem (Simplicial volume and connected sums) 4.3.
Let  and
and  be oriented closed connected manifolds of dimension at least
be oriented closed connected manifolds of dimension at least  . Then
. Then
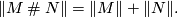
Notice that simplicial volume in general is not additive with respect to connected sums in dimension  : The simplicial volume of the torus is zero (see above), but the simplicial volume of an oriented closed connected surface of genus
: The simplicial volume of the torus is zero (see above), but the simplicial volume of an oriented closed connected surface of genus  is non-zero (see above) is non-zero.
is non-zero (see above) is non-zero.
The proof of Theorem 4.3 is based on the mapping theorem in bounded cohomology (Theorem 5.1) and a careful analysis of so-called tree-like complexes [Gromov1982, Section 3.5]. Generalising these arguments, it can be seen that also additivity for simplicial volume with respect to certain "amenable" gluings holds [Kuessner2001].
4.4 Fibre bundles
- In low dimensions, there is a relation between the simplicial volume of the total space of a fibre bundle of oriented closed connected manifolds and the product of the simplicial volume of base and fibre [Hoster&Kotschick2001][Bucher-Karlsson2009].
- However, in general, the simplicial volume of a fibre bundle of oriented closed connected manifolds is not related in an obvious way to the simplicial volume of base and fibre [Hoster&Kotschick2001]: There exist oriented closed connected hyperbolic
 -manifolds that fibre over the circle. However, the circle has simplicial volume equal to zero, while the simplicial volume of the hyperbolic
-manifolds that fibre over the circle. However, the circle has simplicial volume equal to zero, while the simplicial volume of the hyperbolic  -manifold in question is non-zero (Theorem 3.3).
-manifold in question is non-zero (Theorem 3.3).
- In certain cases, amenable fibres force the simplicial volume to vanish (see below).
4.5 Proportionality principle
For hyperbolic manifolds the simplicial volume is proportional to the Riemannian volume. Gromov and Thurston generalised this result suitably to cover all Riemannian manifolds:
Theorem (Proportionality principle) 4.4.
Let  and
and  be oriented closed connected Riemannian manifolds that have isometric Riemannian universal coverings. Then
be oriented closed connected Riemannian manifolds that have isometric Riemannian universal coverings. Then
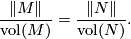
Both Gromov's and Thurston's proof of this result make use of an averaging process. More precisely:
- Gromov's strategy: Use the duality principle (Corollary 3.5) and average (bounded) continuous singular cochains over the isometry group of the Riemannian universal covering modulo the fundamental group; this requires a careful analysis of the relation between (bounded) continuous singular cohomology and (bounded) singular cohomology [Gromov1982, Section 2.3][Bucher-Karlsson2008a][Frigerio2009].
- Thurston's strategy: Replace singular homology by measure homology, and average/smear measure chains over the isometry group of the Riemannian universal covering; this requires a careful analysis of the relation between measure homology and singular homology [Thurston1978, p. 6.9][Löh2005][Löh2006].
5 Simplicial volume and the fundamental group
In view of the duality principle (Corollary 3.5) we can interpret simplicial volume in terms of bounded cohomology. The key to deducing interesting consequences for simplicial volume from bounded cohomology is the relation of bounded cohomology to the fundamental group via the mapping theorem (Theorem 5.1), and the relation of bounded cohomology to geometric group theory (see below).
5.1 Background: Mapping theorem in bounded cohomology
One of the most fundamental (and most surprising) features of bounded cohomology is that it cannot detect amenable groups in the homotopy groups of a space [Gromov1982, Section 3.1][Ivanov1985]:
Theorem (Mapping theorem in bounded cohomology) 5.1.
Let 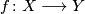 be a (base-point preserving) continuous map between connected countable CW-complexes such that
be a (base-point preserving) continuous map between connected countable CW-complexes such that 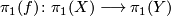 is surjective and has amenable kernel.
is surjective and has amenable kernel.
- Then the induced map
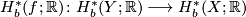 in bounded cohomology is an isometric isomorphism.
in bounded cohomology is an isometric isomorphism.
- In particular, the map
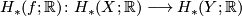 is isometric with respect to the
is isometric with respect to the  -semi-norm
-semi-norm 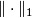 . (In general, this does not say anything about injectivity/surjectivity of
. (In general, this does not say anything about injectivity/surjectivity of 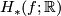 ).
).
Notice however that simplicial volume does not depend only on the fundamental group, but rather on the classifying map to  ; for instance, any oriented closed connected hyperbolic manifold
; for instance, any oriented closed connected hyperbolic manifold  satisfies
satisfies

More generally, if  is an oriented closed connected
is an oriented closed connected  -manifold whose fundamental group has (rational) cohomological dimension less than
-manifold whose fundamental group has (rational) cohomological dimension less than  , then
, then 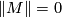 .
.
5.2 Amenability and vanishing results
Direct consequences of the mapping theorem for bounded cohomology (Theorem 5.1) are:
- The simplicial volume of oriented closed connected manifolds with amenable fundamental group is zero;
- this includes, in particular, the case of trivial, Abelian, solvable, and nilpotent fundamental groups.
- Let
 be an oriented closed connected manifold that is the total space of a fibration whose base and fibre are oriented closed connected manifolds (of non-zero dimension), and where the fibre has amenable fundamental group. Then
be an oriented closed connected manifold that is the total space of a fibration whose base and fibre are oriented closed connected manifolds (of non-zero dimension), and where the fibre has amenable fundamental group. Then 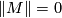 [Lück2002, Exercise 14.15 and p. 556].
[Lück2002, Exercise 14.15 and p. 556].
More generally: A stronger vanishing result for the comparison map 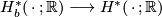 for spaces with amenable coverings of small multiplicity, [Gromov1982, Vanishing Finiteness Theorem on p. 58][Ivanov1985, Corollary 6.3], leads to the following statement: If
for spaces with amenable coverings of small multiplicity, [Gromov1982, Vanishing Finiteness Theorem on p. 58][Ivanov1985, Corollary 6.3], leads to the following statement: If  is an oriented closed connected
is an oriented closed connected  -manifold that admits a covering by amenable open subsets of multiplicity at most
-manifold that admits a covering by amenable open subsets of multiplicity at most  , then
, then 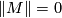 .
.
5.3 Hyperbolicity and non-vanishing results
The non-vanishing of the simplicial volume of Riemannian manifolds with negative sectional curvature (Theorem 3.3) together with the duality principle implies that the cohomological fundamental class of such a manifold lies in the image of the comparison map 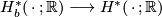 . More generally, Mineyev showed that (in the case of rationally essential manifolds) the condition of negative sectional curvature can be relaxed to word hyperbolicity of the fundamental group [Mineyev2001][Mineyev2002]:
. More generally, Mineyev showed that (in the case of rationally essential manifolds) the condition of negative sectional curvature can be relaxed to word hyperbolicity of the fundamental group [Mineyev2001][Mineyev2002]:
Theorem (Bounded cohomology and word hyperbolic groups) 5.2.
Let  be a finitely presented group. Then the following are equivalent:
be a finitely presented group. Then the following are equivalent:
- The group
 is word hyperbolic.
is word hyperbolic.
- The comparison map
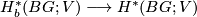 is surjective for all
is surjective for all 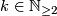 and all Banach
and all Banach  -modules
-modules  .
.
Corollary (Simplicial volume and word hyperbolic fundamental groups) 5.3.
Let  be an oriented closed connected manifold of dimension at least
be an oriented closed connected manifold of dimension at least  that is rationally essential (e.g., aspherical). If the fundamental group of
that is rationally essential (e.g., aspherical). If the fundamental group of  is word hyperbolic, then
is word hyperbolic, then 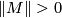 .
.
6 Variations of simplicial volume
For simplicity, in the previous sections we only considered the case that all manifolds in question were orientable and closed (and connected). In the following, we briefly list possible extensions of the definition of simplicial volume to larger classes of manifolds.
6.1 Simplicial volume of manifolds with boundary
For oriented connected compact  -manifolds
-manifolds 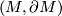 with boundary, the relative simplicial volume
with boundary, the relative simplicial volume 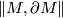 is defined as the
is defined as the  -semi-norm on relative singular homology
-semi-norm on relative singular homology 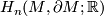 of the relative fundamental class
of the relative fundamental class ![[M,\partial M] \in H_n(M,\partial M;\mathbb{R})](/images/math/0/e/f/0efbf401355cedff3224abca9d9b5de6.png) [Gromov1982][Kuessner2001]; the extension of simplicial volume to manifolds with boundary plays an important role in the theory of
[Gromov1982][Kuessner2001]; the extension of simplicial volume to manifolds with boundary plays an important role in the theory of  -manifolds (see below).
-manifolds (see below).
6.2 Simplicial volume of non-compact manifolds
Non-compact, oriented, connected manifolds have a fundamental class in locally finite homology; notice that there is a (possibly infinite)  -semi-norm on locally finite homology with real coefficients. There are two main flavours of simplicial volumes of non-compact manifolds -- a topological one and a geometric one (where a Lipschitz condition is imposed on the fundamental cycles):
-semi-norm on locally finite homology with real coefficients. There are two main flavours of simplicial volumes of non-compact manifolds -- a topological one and a geometric one (where a Lipschitz condition is imposed on the fundamental cycles):
- Topological version [Gromov1982]: Let
 be an oriented connected
be an oriented connected  -manifold without boundary, and let
-manifold without boundary, and let ![[M] \in H^{\text{lf}}_n(M;\mathbb{R})](/images/math/d/e/3/de3ddfce5b9463ab0f29f3a4cd35d96e.png) be its locally finite fundamental class (with real coefficients). Then the simplicial volume
be its locally finite fundamental class (with real coefficients). Then the simplicial volume 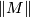 of
of  is defined as the
is defined as the  -semi-norm of
-semi-norm of ![[M]](/images/math/f/a/0/fa08c3d5d2f54260952acc8a646b5025.png) .
.
- For all proper continuous maps
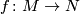 between oriented connected manifolds without boundary of the same dimension we have the inequality
between oriented connected manifolds without boundary of the same dimension we have the inequality 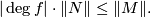
- Notice that the simplicial volume of non-compact manifolds can be infinite; e.g.,
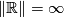 . In particular, if
. In particular, if 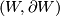 is an oriented compact connected manifold with boundary, then in general the simplicial volume of the interior
is an oriented compact connected manifold with boundary, then in general the simplicial volume of the interior 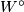 and the relative simplicial volume of
and the relative simplicial volume of 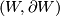 (which is always finite) do not coincide; the finiteness of
(which is always finite) do not coincide; the finiteness of 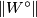 can be characterised in terms of
can be characterised in terms of  -homology [Löh2008].
-homology [Löh2008].
- However, the simplicial volume of non-compact manifolds vanishes for many interesting manifolds [Gromov1982, p. 58f][Löh&Sauer2009], and it does not behave well with respect to taking products: for instance,
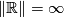 , but
, but 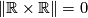 [Gromov1982, p. 8f][Löh2008].
[Gromov1982, p. 8f][Löh2008].
- For all proper continuous maps
 be an oriented connected Riemannian
be an oriented connected Riemannian  -manifold. Then the Lipschitz simplicial volume of
-manifold. Then the Lipschitz simplicial volume of  is defined by
is defined by
![\displaystyle \|M\|_{\text{Lip}} := \inf \bigl\{ |c|_1 \bigm| \text{$c \in C^{\text{lf}}_n(M;\mathbb{R})$ is a fundamental cycle of~$M$ with $\mathrm{Lip}(c) < \infty$} \bigr\} \in [0,\infty],](/images/math/1/6/0/160b90f47a327c84fc64248d46789605.png)
where, 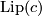 is the supremum of the Lipschitz constants of all singular simplices occurring in
is the supremum of the Lipschitz constants of all singular simplices occurring in  .
.
- Lipschitz simplicial volume is functorial with respect to proper Lipschitz maps between Riemannian manifolds of the same dimension (so, one application of the Lipschitz simplicial volume are degree theorems for proper Lipschitz maps between non-compact manifolds [Löh&Sauer2009]).
- The Lipschitz simplicial volume is (up to a dimension constant) a lower bound for the minimal volume [Gromov1982].
- The Lipschitz simplicial volume of locally symmetric spaces of finite volume and non-compact type is non-zero [Löh&Sauer2009].
- The Lipschitz simplicial volume of Hilbert modular varieties coincides with the simplicial volume [Löh&Sauer2009a].
- The Lipschitz simplicial volume behaves better than the topologically defined simplicial volume with respect to taking products [Löh&Sauer2009], and there is a version of the proportionality principle for the Lipschitz simplicial volume [Gromov1982, p. 80][Löh&Sauer2009].
6.3 Simplicial volume of non-orientable manifolds
The simplicial volume of a connected non-orientable manifold  is defined as
is defined as 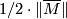 , where
, where 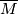 is the orientation double covering of
is the orientation double covering of  ; in view of the multiplicativity of the simplicial volume (of oriented manifolds) with respect to finite coverings, this definition is reasonable.
; in view of the multiplicativity of the simplicial volume (of oriented manifolds) with respect to finite coverings, this definition is reasonable.
7 Applications
Typically, simplicial volume is used as a tool to establish topological rigidity properties of the Riemannian volume or non-vanishing of the minimal volume of certain manifolds. Two prominent examples are Gromov's proof of Mostow rigidity and degree theorems.
7.1 Mostow rigidity
Hyperbolic manifolds are completely determined by their homotopy type, i.e., hyperbolic manifolds are rigid in the following sense [Mostow1968]:
Theorem (Mostow rigidity) 7.1.
Let  and
and  be oriented closed connected hyperbolic manifolds of the same dimension
be oriented closed connected hyperbolic manifolds of the same dimension 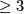 . If
. If 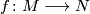 is a homotopy equivalence, then there is an isometry
is a homotopy equivalence, then there is an isometry 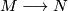 homotopic to
homotopic to  .
In particular, any oriented closed connected smooth manifold of dimension at least
.
In particular, any oriented closed connected smooth manifold of dimension at least  can admit at most one hyperbolic structure.
can admit at most one hyperbolic structure.
One decisive step in Gromov's proof [Munkholm1980][Benedetti&Petronio1992, Chapter C][Ratcliffe1994, Chapter 11] of Mostow rigidity is to show that if two oriented closed connected hyperbolic manifolds are homotopy equivalent, they have to have the same volume; Gromov introduced simplicial volume in this context as it provides an elegant way of establishing this fact (using the relation to the hyperbolic volume (Theorem 3.3) and the functoriality of the simplicial volume (Corollary 2.2)).
7.2 Degree theorems
A degree theorem is a theorem of the following form:
Metatheorem (Degree theorem) 7.2.
Let 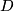 and
and  be certain suitable classes of Riemannian manifolds of the same dimension -- the domain manifolds and the target manifolds. Then there is a constant
be certain suitable classes of Riemannian manifolds of the same dimension -- the domain manifolds and the target manifolds. Then there is a constant 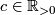 with the following property: For all
with the following property: For all 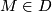 , all
, all 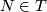 and all continuous maps
and all continuous maps 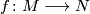 we have
we have
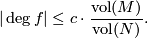
The art is to find suitable classes of domain and target manifolds. The functoriality of simplicial volume (Corollary 2.2) and the relationship between the Riemannian volume of closed hyperbolic manifolds and the simplicial volume (Theorem 3.3) combine to give a degree theorem for hyperbolic manifolds:
Degree theorem for hyperbolic manifolds 7.3.
Let  and
and  be oriented closed connected hyperbolic manifolds of the same dimension. Then
be oriented closed connected hyperbolic manifolds of the same dimension. Then
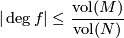
holds for any continuous map 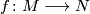 .
.
In a similar way, non-vanishing results for simplicial volume together with Gromov's estimate of the minimal volume in terms of the simplicial volume give rise to more general degree theorems [Gromov1982, Section 0.5][Lafont&Schmidt2006] (complementing and extending the original degree theorem in higher rank by Connell and Farb [Connell&Farb2003]), and parallel results for the Lipschitz simplicial volume of non-compact Riemannian manifolds lead to degree theorems for proper Lipschitz maps between certain non-compact manifolds [Löh&Sauer2009] (complementing and extending the degree theorem by Connell and Farb [Connell&Farb2003]).
7.3 Dehn fillings and Riemannian volume
Using the relation between the simplicial volume of hyperbolic manifolds and the hyperbolic volume (a generalised version that also covers non-compact manifolds and manifolds with boundary), Thurston proved that hyperbolic Dehn fillings of complete hyperbolic  -manifolds of finite volume decrease the Riemannian volume [Thurston1978, Theorem 6.5.6].
-manifolds of finite volume decrease the Riemannian volume [Thurston1978, Theorem 6.5.6].
7.4 Recognising graph manifolds
Simplicial volume recognises graph manifolds:
- The gluing formula for gluings along tori [Gromov1982][Kuessner2001], the fact that the simplicial volume of hyperbolic manifolds is proportional to the Riemannian volume, and the fact that the simplicial volume of Seifert
 -manifolds is zero show that the simplicial volume of a
-manifolds is zero show that the simplicial volume of a  -manifold (possibly with boundary) that has a geometric decomposition is proportional to the sum of the volumes of the hyperbolic pieces in such a decomposition. Therefore, a
-manifold (possibly with boundary) that has a geometric decomposition is proportional to the sum of the volumes of the hyperbolic pieces in such a decomposition. Therefore, a  -manifold that has a geometric decomposition is a graph manifold if and only if it has zero simplicial volume. (Together with Perelman's proof of geometrisation for
-manifold that has a geometric decomposition is a graph manifold if and only if it has zero simplicial volume. (Together with Perelman's proof of geometrisation for  -manifolds this means that a
-manifolds this means that a  -manifold is a graph manifold if and only if it has zero simplicial volume.)
-manifold is a graph manifold if and only if it has zero simplicial volume.)
- In a similar spirit, one can show the following: Let
 be a Haken
be a Haken  -manifold whose boundary is a union of tori such that any manifold obtained from
-manifold whose boundary is a union of tori such that any manifold obtained from  by Dehn fillings has simplicial volume equal to zero. Then
by Dehn fillings has simplicial volume equal to zero. Then  is a graph manifold [Boileau&Leeb&Porti2005, Proposition 10.17][Boileau&Maillot&Porti2003, Proposition 9.36]. This result is used in an alternative proof [Bessières&Besson&Boileau&Maillot&Porti2007] of the last step in Perelman's proof of the Geometrisation Conjecture for aspherical
is a graph manifold [Boileau&Leeb&Porti2005, Proposition 10.17][Boileau&Maillot&Porti2003, Proposition 9.36]. This result is used in an alternative proof [Bessières&Besson&Boileau&Maillot&Porti2007] of the last step in Perelman's proof of the Geometrisation Conjecture for aspherical  -manifolds.
-manifolds.
7.5 A conjecture on the simplicial volume of knot complements
H. Murakami and J. Murakami conjectured, similar to the volume conjecture for knots [Kashaev1997], that the simplicial volume of a knot complement should be related to the asymptotic growth rate of the coloured Jones polynomials of the knot in question [Murakami&Murakami2001, Conjecture 5.1]; if this conjecture holds, then the (finite type) Vassiliev invariants are able to detect triviality of a knot [Murakami&Murakami2001].
8 References
- [Belegradek2006] I. Belegradek, Aspherical manifolds, relative hyperbolicity, simplicial volume and assembly maps, Algebr. Geom. Topol. 6 (2006), 1341–1354 (electronic). MR2253450 (2007f:57004) Zbl 1137.20035
- [Benedetti&Petronio1992] R. Benedetti and C. Petronio, Lectures on hyperbolic geometry, Springer-Verlag, Berlin, 1992. MR1219310 (94e:57015) Zbl 0768.51018
- [Bessières&Besson&Boileau&Maillot&Porti2007] L. Bessières, G. Besson, M. Boileau, S. Maillot and J. Porti, Weak collapsing and geometrisation of aspherical 3-manifolds, (2007). Available at the arXiv:0706.2065.
- [Besson&Courtois&Gallot1991] G. Besson, G. Courtois and S. Gallot, Volume et entropie minimale des espaces localement symétriques, Invent. Math. 103 (1991), no.2, 417–445. MR1085114 (92d:58027) Zbl 0723.53029
- [Boileau&Leeb&Porti2005] M. Boileau, B. Leeb and J. Porti, Geometrization of 3-dimensional orbifolds, Ann. of Math. (2) 162 (2005), no.1, 195–290. MR2178962 (2007f:57028) Zbl 1087.57009
- [Boileau&Maillot&Porti2003] M. Boileau, S. Maillot and J. Porti, Three-dimensional orbifolds and their geometric structures, Société Mathématique de France, 2003. MR2060653 (2005b:57030) Zbl 1058.57009
- [Brooks1978] R. Brooks, Some remarks on bounded cohomology, in Riemann surfaces and related topics: Proceedings of the 1978 Stonybrook Conference, Ann. of Math. Stud., 97 (1978), 53–63. MR624804 (83a:57038) Zbl 0457.55002
- [Bucher-Karlsson2008] M. Bucher-Karlsson, The simplicial volume of closed manifolds covered by
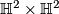 , J. Topol. 1 (2008), no.3, 584–602. MR2417444 (2009i:53025) Zbl 1156.53018
, J. Topol. 1 (2008), no.3, 584–602. MR2417444 (2009i:53025) Zbl 1156.53018
- [Bucher-Karlsson2008a] M. Bucher-Karlsson, The proportionality constant for the simplicial volume of locally symmetric spaces, Colloq. Math. 111 (2008), no.2, 183–198. MR2365796 (2008k:53105) Zbl 1187.53042
- [Bucher-Karlsson2009] M. Bucher-Karlsson, Simplicial volume of products and fiber bundles, in Discrete Groups and Geometric Structures (Kortrijk, 2008), K. Dekimpe, P.Igodt, A. Valette (Edts.), Contemporary Mathematics, AMS, 2009. MR2581916 Zbl 1203.55008
- [Bühler2008] T. Bühler, A derived functor approach to bounded cohomology, C. R. Math. Acad. Sci. Paris 346 (2008), no.11-12, 615–618. MR2423264 (2009f:18013) Zbl 1148.18007
- [Connell&Farb2003] C. Connell and B. Farb, The degree theorem in higher rank, J. Differential Geom. 65 (2003), no.1, 19–59. MR2057530 (2005d:53064) Zbl 1067.53032
- [Frigerio2009] R. Frigerio, (Bounded) continuous cohomology and Gromov proportionality principle, (2009). Available at the arXiv:0903.4412.
- [Gromov1982] M. Gromov, Volume and bounded cohomology, Inst. Hautes Études Sci. Publ. Math. (1982), no.56, 5–99 (1983). MR686042 (84h:53053) Zbl 0516.53046
- [Gromov1999] M. Gromov, Metric structures for Riemannian and non-Riemannian spaces, Birkhäuser Boston Inc., Boston, MA, 1999. MR1699320 (2000d:53065) Zbl 1113.53001
- [Hoster&Kotschick2001] M. Hoster and D. Kotschick, On the simplicial volumes of fiber bundles, Proc. Amer. Math. Soc. 129 (2001), no.4, 1229–1232. MR1709754 (2001g:55012) Zbl 0981.53022
- [Inoue&Yano1982] H. Inoue and K. Yano, The Gromov invariant of negatively curved manifolds, Topology 21 (1982), no.1, 83–89. MR630882 (82k:53091) Zbl 0469.53038
- [Ivanov1985] N. V. Ivanov, Foundations of the theory of bounded cohomology, Zap. Nauchn. Sem. Leningrad. Otdel. Mat. Inst. Steklov. (LOMI) 143 (1985), 69–109, 177. MR806562 (87b:53070) Zbl 0612.55006
- [Kashaev1997] R. M. Kashaev, The hyperbolic volume of knots from the quantum dilogarithm, Lett. Math. Phys. 39 (1997), no.3, 269–275. MR1434238 (98b:57012) Zbl 0876.57007
- [Kuessner2001] T. Kuessner, Relative simplicial volume, PhD thesis, Tübingen, 2001.
- [Lafont&Schmidt2006] J. Lafont and B. Schmidt, Simplicial volume of closed locally symmetric spaces of non-compact type, Acta Math. 197 (2006), no.1, 129–143. MR2285319 (2007k:53033) Zbl 1111.57020
- [Löh&Sauer2009] C. Löh and R. Sauer, Degree theorems and Lipschitz simplicial volume for nonpositively curved manifolds of finite volume, J. Topol. 2 (2009), no.1, 193–225. MR2499443 (197) Zbl 1187.53043
- [Löh&Sauer2009a] C. Löh and R. Sauer, Simplicial volume of Hilbert modular varieties, Comment. Math. Helv. 84 (2009), no.3, 457–470. MR2507250 (References) Zbl 1180.53046
- [Löh2005] C. Löh, The Proportionality Principle of Simplicial Volume, (2005). Available at the arXiv:0504106, diploma thesis, WWU Münster, 2004.
- [Löh2006] C. Löh, Measure homology and singular homology are isometrically isomorphic, Math. Z. 253 (2006), no.1, 197–218. MR2206643 (2006m:55021) Zbl 1093.55004
- [Löh2008] C. Löh, Isomorphisms in
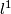 -homology, Münster J. Math. 1 (2008), 237–265. MR2502500 (2010b:55007) Zbl 1158.55007
-homology, Münster J. Math. 1 (2008), 237–265. MR2502500 (2010b:55007) Zbl 1158.55007
- [Lück2002] W. Lück,
 -invariants: theory and applications to geometry and
-invariants: theory and applications to geometry and  -theory, Springer-Verlag, Berlin, 2002. MR1926649 (2003m:58033) Zbl 1009.55001
-theory, Springer-Verlag, Berlin, 2002. MR1926649 (2003m:58033) Zbl 1009.55001
- [Mineyev2001] I. Mineyev, Straightening and bounded cohomology of hyperbolic groups, Geom. Funct. Anal. 11 (2001), no.4, 807–839. MR1866802 (2002k:20078) Zbl 1013.20034
- [Mineyev2002] I. Mineyev, Bounded cohomology characterizes hyperbolic groups, Q. J. Math. 53 (2002), no.1, 59–73. MR1887670 (2003k:20088) Zbl 1013.20048
- [Monod2001] N. Monod, Continuous bounded cohomology of locally compact groups, Springer-Verlag, Berlin, 2001. MR1840942 (2002h:46121) Zbl 0967.22006
- [Monod2006] N. Monod, An invitation to bounded cohomology, International Congress of Mathematicians. Vol. II, Eur. Math. Soc., Zürich, (2006), 1183–1211. MR2275641 (2008e:22011) Zbl 1127.55002
- [Mostow1968] G. D. Mostow, Quasi-conformal mappings in
 -space and the rigidity of hyperbolic space forms, Inst. Hautes Études Sci. Publ. Math. (1968), no.34, 53–104. MR0236383 (38 #4679) Zbl 0238.30022
-space and the rigidity of hyperbolic space forms, Inst. Hautes Études Sci. Publ. Math. (1968), no.34, 53–104. MR0236383 (38 #4679) Zbl 0238.30022
- [Munkholm1980] H. J. Munkholm, Simplices of maximal volume in hyperbolic space, Gromov's norm, and Gromov's proof of Mostow's rigidity theorem (following Thurston), 788 (1980), 109–124. MR585656 (81k:53046) Zbl 0434.57017
- [Murakami&Murakami2001] H. Murakami and J. Murakami, The colored Jones polynomials and the simplicial volume of a knot, Acta Math. 186 (2001), no.1, 85–104. MR1828373 (2002b:57005) Zbl 0983.57009
- [Noskov1990] G. A. Noskov, Bounded cohomology of discrete groups with coefficients, Algebra i Analiz 2 (1990), no.5, 146–164. MR1086449 (92b:57005) Zbl 0729.55005
- [Ratcliffe1994] J. G. Ratcliffe, Foundations of hyperbolic manifolds, Springer-Verlag, New York, 1994. MR1299730 (95j:57011) Zbl 1106.51009
- [Thurston1978] W. P. Thurston, The Geometry and Topology of 3-Manifolds. Lecture notes, Princeton, 1978.
- [Yano1982] K. Yano, Gromov invariant and
 -actions, J. Fac. Sci. Univ. Tokyo Sect. IA Math. 29 (1982), no.3, 493–501.
-actions, J. Fac. Sci. Univ. Tokyo Sect. IA Math. 29 (1982), no.3, 493–501.
9 External Links
- The Wikipedia page on simplicial volume.