Simplicial volume
(→Definition and history) |
|||
| Line 38: | Line 38: | ||
</wikitex> | </wikitex> | ||
| − | + | == Functoriality and elementary examples == | |
| − | + | <wikitex> | |
| − | + | The $\ell^1$-semi-norm is functorial in the following sense {{cite|Gromov1999}}: | |
| − | + | ||
| − | + | ||
| − | = | + | {{Beginthm|Proposition}} |
| + | If $f \colon X \longrightarrow Y$ is a continuous map of topological spaces and $\alpha \in H_*(X;\mathbb{R})$, then | ||
| + | $$ \bigl\| H_*(f;\mathbb{R}) (\alpha) \bigr\|_1 \leq \|\alpha\|_1,$$ | ||
| + | as can be seen by inspecting the definition of $H_*(f;\mathbb{R}) = H_*(C_*(f;\mathbb{R}))$ and of $\|\cdot\|_1$. | ||
| + | {{Endthm}} | ||
| − | + | {{Beginthm|Corollary}} | |
| − | + | * Let $f \colon M\longrightarrow N$ be a map of oriented closed connected manifolds of the same dimension. Then | |
| − | + | $$ |\deg f| \cdot \|N\| \leq \|M\|.$$ | |
| + | * Because homotopy equivalences of oriented closed connected manifolds have degree $-1$ or $1$, it follows that the simplicial volume indeed is a homotopy invariant of oriented closed connected manifolds. | ||
| + | {{Endthm}} | ||
</wikitex> | </wikitex> | ||
| + | <!-- COMMENT: | ||
| − | + | 2do! | |
| + | add references | ||
| + | complete the following sections | ||
| + | add intro/history | ||
== "Computing" Simplicial volume == | == "Computing" Simplicial volume == | ||
Revision as of 15:13, 23 March 2010
|
An earlier version of this page was published in the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 09:51, 1 April 2011 and the changes since publication. |
|
The user responsible for this page is Clara Löh. No other user may edit this page at present. |
1 Definition and history
The simplicial volume is a homotopy invariant of oriented closed connected manifolds that was introduced by Gromov in his proof of Mostow rigidity [Munkholm1980][Gromov1982]. Intuitively, the simplicial volume measures how difficult it is to describe the manifold in question in terms of simplices (with real coefficients):
Definition 1.1.
Let  be an oriented closed connected manifold of dimension
be an oriented closed connected manifold of dimension  .
Then the simplicial volume (also called Gromov norm) of
.
Then the simplicial volume (also called Gromov norm) of  is defined as
is defined as
![\displaystyle \|M\| := \bigl\| [M] \bigr\|_1 = \inf \bigl\{ |c|_1 \bigm| \text{$c \in C_n(M;\mathbb{R})$ is a fundamental cycle of $M$} \bigr\} \in \mathbb{R}_{\geq 0},](/images/math/c/2/2/c22511eadabaaaa5caa7565812d6977a.png)
where ![[M] \in H_n(M;\mathbb{R})](/images/math/7/d/7/7d74a20a6efc50970d884cfa1c1e5861.png) is the fundamental class of
is the fundamental class of  with real coefficients.
with real coefficients.
- Here,
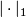 denotes the
denotes the  -norm on the singular chain complex
-norm on the singular chain complex 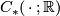 with real coefficients induced from the (unordered) basis given by all singular simplices, i.e.: for a topological space
with real coefficients induced from the (unordered) basis given by all singular simplices, i.e.: for a topological space  and a chain
and a chain 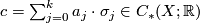 (in reduced form), the
(in reduced form), the  -norm of
-norm of  is given by
is given by
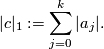
- Moreover,
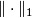 denotes the
denotes the  -semi-norm on singular homology
-semi-norm on singular homology 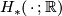 with real coefficients, which is induced by
with real coefficients, which is induced by 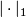 . More explicitly, if
. More explicitly, if  is a topological space and
is a topological space and 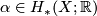 , then
, then
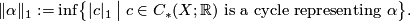
2 Functoriality and elementary examples
The  -semi-norm is functorial in the following sense [Gromov1999]:
-semi-norm is functorial in the following sense [Gromov1999]:
Proposition 2.1.
If 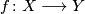 is a continuous map of topological spaces and
is a continuous map of topological spaces and 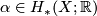 , then
, then
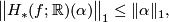
as can be seen by inspecting the definition of 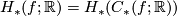 and of
and of 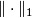 .
.
Corollary 2.2.
- Let
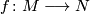 be a map of oriented closed connected manifolds of the same dimension. Then
be a map of oriented closed connected manifolds of the same dimension. Then
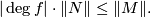
- Because homotopy equivalences of oriented closed connected manifolds have degree
 or
or  , it follows that the simplicial volume indeed is a homotopy invariant of oriented closed connected manifolds.
, it follows that the simplicial volume indeed is a homotopy invariant of oriented closed connected manifolds.
3 References
- [Gromov1982] M. Gromov, Volume and bounded cohomology, Inst. Hautes Études Sci. Publ. Math. (1982), no.56, 5–99 (1983). MR686042 (84h:53053) Zbl 0516.53046
- [Gromov1999] M. Gromov, Metric structures for Riemannian and non-Riemannian spaces, Birkhäuser Boston Inc., Boston, MA, 1999. MR1699320 (2000d:53065) Zbl 1113.53001
- [Munkholm1980] H. J. Munkholm, Simplices of maximal volume in hyperbolic space, Gromov's norm, and Gromov's proof of Mostow's rigidity theorem (following Thurston), 788 (1980), 109–124. MR585656 (81k:53046) Zbl 0434.57017
|
This page has not been refereed. The information given here might be incomplete or provisional. |