Simplicial volume
(Undo revision 2158 by Diarmuid Crowley (Talk)) |
(Created page with '<!-- COMMENT: To achieve a unified layout, along with using the template below, please OBSERVE the following: besides, $...$ and $$...$$, you should use two environments: - Fo…') |
||
| Line 16: | Line 16: | ||
== Definition and history == | == Definition and history == | ||
<wikitex>; | <wikitex>; | ||
| + | |||
| + | The ''simplicial volume'' is a homotopy invariant of oriented closed connected manifolds that was introduced by Gromov in his proof of Mostow rigidity {{cite|Munkholm1980}}{{cite|Gromov1982}}. Intuitively, the simplicial volume measures how difficult it is to describe the manifold in question in terms of simplices (with real coefficients): | ||
{{Beginthm|Definition}} | {{Beginthm|Definition}} | ||
| Line 37: | Line 39: | ||
<wikitex>; | <wikitex>; | ||
| − | + | ||
| + | |||
| + | |||
</wikitex> | </wikitex> | ||
| Line 61: | Line 65: | ||
=== Non-vanishing results === | === Non-vanishing results === | ||
| + | |||
== Applications == | == Applications == | ||
| Line 83: | Line 88: | ||
{{#RefList:}} | {{#RefList:}} | ||
| − | [[Category: | + | [[Category:Theory]] |
{{Stub}} | {{Stub}} | ||
Revision as of 15:39, 10 March 2010
|
An earlier version of this page was published in the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 09:51, 1 April 2011 and the changes since publication. |
|
The user responsible for this page is Clara Löh. No other user may edit this page at present. |
1 Definition and history
The simplicial volume is a homotopy invariant of oriented closed connected manifolds that was introduced by Gromov in his proof of Mostow rigidity [Munkholm1980][Gromov1982]. Intuitively, the simplicial volume measures how difficult it is to describe the manifold in question in terms of simplices (with real coefficients):
Definition 1.1.
Let  be an oriented closed connected manifold of dimension
be an oriented closed connected manifold of dimension  . Then the simplicial volume (also called Gromov norm) of
. Then the simplicial volume (also called Gromov norm) of  is defined as
is defined as
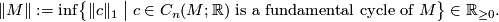
Here, 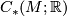 denotes the singular chain complex of
denotes the singular chain complex of  with real coefficients, and
with real coefficients, and 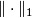 denotes the
denotes the  -norm on the singular chain complex induced from the (unordered) basis given by all singular simplices; i.e., for a chain
-norm on the singular chain complex induced from the (unordered) basis given by all singular simplices; i.e., for a chain 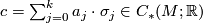 (in reduced form), the
(in reduced form), the  -norm of
-norm of  is given by
is given by
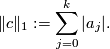
2 References
- [Gromov1982] M. Gromov, Volume and bounded cohomology, Inst. Hautes Études Sci. Publ. Math. (1982), no.56, 5–99 (1983). MR686042 (84h:53053) Zbl 0516.53046
- [Munkholm1980] H. J. Munkholm, Simplices of maximal volume in hyperbolic space, Gromov's norm, and Gromov's proof of Mostow's rigidity theorem (following Thurston), 788 (1980), 109–124. MR585656 (81k:53046) Zbl 0434.57017
|
This page has not been refereed. The information given here might be incomplete or provisional. |