Simplicial volume
(Difference between revisions)
| Line 1: | Line 1: | ||
| − | + | {{Authors|Crowley}} | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
== Definition and history == | == Definition and history == | ||
<wikitex>; | <wikitex>; | ||
Revision as of 12:47, 10 March 2010
|
An earlier version of this page was published in the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 09:51, 1 April 2011 and the changes since publication. |
|
The user responsible for this page is Crowley. No other user may edit this page at present. |
1 Definition and history
Definition 1.1.
Let  be an oriented closed connected manifold of dimension
be an oriented closed connected manifold of dimension  . Then the simplicial volume (also called Gromov norm) of
. Then the simplicial volume (also called Gromov norm) of  is defined as
is defined as
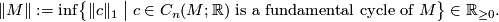
Here, 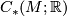 denotes the singular chain complex of
denotes the singular chain complex of  with real coefficients, and
with real coefficients, and 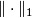 denotes the
denotes the  -norm on the singular chain complex induced from the (unordered) basis given by all singular simplices; i.e., for a chain
-norm on the singular chain complex induced from the (unordered) basis given by all singular simplices; i.e., for a chain 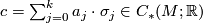 (in reduced form), the
(in reduced form), the  -norm of
-norm of  is given by
is given by
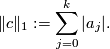
2 References
|
This page has not been refereed. The information given here might be incomplete or provisional. |