Simple closed curves in surfaces (Ex)

Latest revision as of 04:46, 7 January 2019

Let $<wikitex>; Let $\Sigma_g$ be a closed oriented surface of genus $g$ and let $\alpha_1, \dots, \alpha_g \subset \Sigma_g$ be pair-wise disjoint simple closed curves. Prove that the homology classes $\{[\alpha_1], \dots [\alpha_g]\} \subset H_1(\Sigma_g; \Z/2)$ are linearly independent if the complement $\Sigma_g \setminus \cup_{i=1}^g \alpha_i$ is connected. 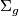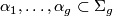</wikitex> [[Category:Exercises]] [[Category:Exercises without solution]]\Sigma_g$ be a closed oriented surface of genus $g$ and let $\alpha_1, \dots, \alpha_g \subset \Sigma_g$ be pair-wise disjoint simple closed curves. 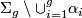Prove that the set of homology classes $\{[\alpha_1], \dots [\alpha_g]\} \subset H_1(\Sigma_g; \Z/2)$ is linearly independent if the complement $\Sigma_g \setminus \cup_{i=1}^g \alpha_i$ is connected.

Does the converse hold?