Talk:Simple closed curves in surfaces (Ex)
Suppose that 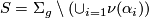 is connected. We will construct a dual basis
is connected. We will construct a dual basis  as usual and then use the intersection pairing
as usual and then use the intersection pairing  on
on 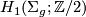 to see that the
to see that the ![[\alpha_i]](/images/math/7/b/6/7b67facef53372793b83affae25d8f18.png) are linearly independent.
are linearly independent.
Deleting an annulus from a surface preserves Euler characteristic, so 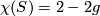 , and
, and  has
has 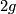 boundary components (in pairs corresponding to each
boundary components (in pairs corresponding to each 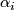 ). Thus,
). Thus, 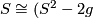 disks
disks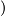 . Let
. Let 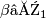 be an arc in
be an arc in  between the two boundary components of
between the two boundary components of 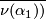 . Extend
. Extend 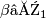 to a loop in
to a loop in  by adding a cocore of the annulus
by adding a cocore of the annulus 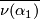 . Now
. Now 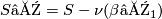 is another planar surface, so we repeat the argument in turn to find loops
is another planar surface, so we repeat the argument in turn to find loops  in
in  so that for
so that for 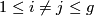 , we have
, we have 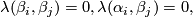 and
and 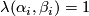 .
.
Now suppose for some 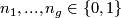 ,
, ![w=\sum_{i=1}^g n_i[\alpha_i]](/images/math/8/9/7/897a216441ce4b0e4a1ddd0630c88a47.png) is the identity in
is the identity in 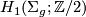 . Then
. Then 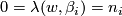 for each
for each  . Thus,
. Thus, ![[\alpha_1],...,[\alpha_g]](/images/math/6/1/b/61b445c545fd209b45a80658d341e182.png) are linearly independent.
are linearly independent.
The converse holds as well. That is, suppose instead that  is disconnected. Let
is disconnected. Let  be one component of
be one component of  , and let
, and let 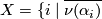 meets
meets  in exactly one boundary component
in exactly one boundary component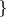 . Since
. Since  has multiple components,
has multiple components,  is nonempty. Let
is nonempty. Let 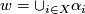 . Then
. Then  bounds in
bounds in  (up to reorienting some
(up to reorienting some 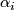 ), so
), so ![[w]=\sum_{i\in X}[\alpha_i]=[0]\in H_1(\Sigma_g;\mathbb{Z}/2)](/images/math/f/c/2/fc28a43e9b2526e6832ba6b636772534.png) . Thus,
. Thus, ![[\alpha_1],...,[\alpha_g]](/images/math/6/1/b/61b445c545fd209b45a80658d341e182.png) are linearly dependent.
are linearly dependent.
Alternate method: We can control the number of components by the zeroth homology. First, thicken up the circles given by the curves, so that they become 2D bands. Then use Mayer Vietoris, where the first component is the desired complement 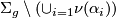 , and the second component is the union of the thickened circles. The purpose of thickening is to provide a workable intersection. Since the group is
, and the second component is the union of the thickened circles. The purpose of thickening is to provide a workable intersection. Since the group is 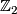 , we can treat the homology as a vector space, which lets us count dimensions. If the curves are linearly dependent, the boundary map from
, we can treat the homology as a vector space, which lets us count dimensions. If the curves are linearly dependent, the boundary map from 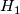 to
to 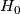 has image whose dimension is smaller than the number of curves (
has image whose dimension is smaller than the number of curves ( ), which then forces the dimension of the zero-th homology of the cut manifold to be at least 2.
), which then forces the dimension of the zero-th homology of the cut manifold to be at least 2.
Note that this alternate method works without modification, if there is a different number of curves (say, 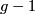 ).
).