S-duality I (Ex)
From Manifold Atlas
(Difference between revisions)
m (moved S-duality I to S-duality I (Ex)) |
Markullmann (Talk | contribs) (Corrections to the exercise statement.) |
||
| Line 1: | Line 1: | ||
<wikitex>; | <wikitex>; | ||
| − | Let $X$ and $Y$ be a finite CW-complexes. A map | + | Let $X$ and $Y$ be a finite pointed CW-complexes. A map |
$$ \alpha \colon S^N \to X \wedge Y $$ | $$ \alpha \colon S^N \to X \wedge Y $$ | ||
is called an S-duality if the slant product induced by $\alpha$ | is called an S-duality if the slant product induced by $\alpha$ | ||
| − | $$ | + | $$ - \backslash \alpha \colon H^i(X; \Zz) \to H_{N-i}(Y;\Zz) $$ |
is an isomorphism for all $i$. In this case $X$ and $Y$ are called an $S$-duals of each other. | is an isomorphism for all $i$. In this case $X$ and $Y$ are called an $S$-duals of each other. | ||
{{beginthm|Exercise}} \label{exrcs:S-duality-property} | {{beginthm|Exercise}} \label{exrcs:S-duality-property} | ||
Latest revision as of 21:01, 28 May 2012
Let  and
and  be a finite pointed CW-complexes. A map
be a finite pointed CW-complexes. A map
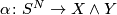
is called an S-duality if the slant product induced by 
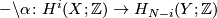
is an isomorphism for all  . In this case
. In this case  and
and  are called an
are called an  -duals of each other.
-duals of each other.
Exercise 0.1.
Show that  -duality satisfies the following"
-duality satisfies the following"
- For every finite CW-complex
 there exists an
there exists an  -dimensional S-dual, which we denote
-dimensional S-dual, which we denote 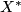 , for some large
, for some large 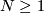 .
.
- If
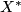 is an
is an  -dimensional
-dimensional  -dual of
-dual of  then
then 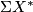 is an
is an 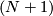 -dimensional
-dimensional  -dual of
-dual of  .
.
- For any space
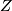 we have isomorphisms
we have isomorphisms
![\displaystyle S \co [X,Z] \cong [S^N,Z \wedge Y] \quad \gamma \mapsto S(\gamma) = (\gamma \wedge \id_Y) \circ \alpha,](/images/math/2/e/3/2e338f16c1b628f5b4a304a519e95c2f.png)
![\displaystyle S \co [Y,Z] \cong [S^N,X \wedge Z] \quad \gamma \mapsto S(\gamma) = (\id_X \wedge \gamma) \circ \alpha.](/images/math/0/4/b/04be7aa3025bba0a81540a78fd977851.png)
- A map
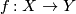 induces a map
induces a map 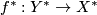 for
for  large enough via the isomorphism
large enough via the isomorphism
![\displaystyle [X,Y] \cong [S^N,Y \wedge X^\ast] \cong [Y^\ast,X^\ast].](/images/math/f/6/f/f6f50e4cf33de39bb6bf0368abcef85a.png)
- If
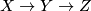 is a cofibration sequence then
is a cofibration sequence then 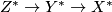 is a cofibration sequence for
is a cofibration sequence for  large enough.
large enough.