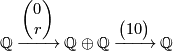Reidemeister torsion (Ex)
From Manifold Atlas
Revision as of 14:01, 29 July 2013 by Diarmuid Crowley (Talk | contribs)
Show that the following finite based free 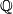 -chain compex concentrated in dimensions
-chain compex concentrated in dimensions  ,
,  and
and  is contractible
and compute its Reidemeister torsion
is contractible
and compute its Reidemeister torsion
References
$ and -chain compex concentrated in dimensions ,
,  and
and  is contractible
and compute its Reidemeister torsion
is contractible
and compute its Reidemeister torsion
References
$ is contractible and compute its Reidemeister torsion $$ \Qq \xrightarrow{\left( \begin{array}{c} 0 \ r \end{array} \right)} \Qq \oplus \Qq \xrightarrow{\left( \begin{array}{cc} 1 & 0 \end{array} \right)} \Qq $$ == References == {{#RefList:}} [[Category:Exercises]] [[Category:Exercises without solution]]\Qq-chain compex concentrated in dimensions ,
,  and
and  is contractible
and compute its Reidemeister torsion
is contractible
and compute its Reidemeister torsion