Talk:Reidemeister torsion (Ex)

Since the chain complex in question is finite and levelwise projective we know that contractibility is implied by being acyclic. And we see directly that if 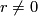$r \neq 0$$\newcommand{\Z}{\mathbb{Z}} \newcommand{\R}{\mathbb{R}} \newcommand{\C}{\mathbb{C}} \newcommand{\N}{\mathbb{N}} \newcommand{\Q}{\mathbb{Q}} \newcommand{\F}{\mathbb{F}} \newcommand{\bZ}{\mathbb{Z}} \newcommand{\bR}{\mathbb{R}} \newcommand{\bC}{\mathbb{C}} \newcommand{\bH}{\mathbb{H}} \newcommand{\bQ}{\mathbb{Q}} \newcommand{\bF}{\mathbb{F}} \newcommand{\bN}{\mathbb{N}} \DeclareMathOperator\id{id} % identity map \DeclareMathOperator\Sq{Sq} % Steenrod squares \DeclareMathOperator\Homeo{Homeo} % group of homeomorphisms of a topoloical space \DeclareMathOperator\Diff{Diff} % group of diffeomorphisms of a smooth manifold \DeclareMathOperator\SDiff{SDiff} % diffeomorphism under some constraint \DeclareMathOperator\Hom{Hom} % homomrphism group \DeclareMathOperator\End{End} % endomorphism group \DeclareMathOperator\Aut{Aut} % automorphism group \DeclareMathOperator\Inn{Inn} % inner automorphisms \DeclareMathOperator\Out{Out} % outer automorphism group \DeclareMathOperator\vol{vol} % volume \newcommand{\GL}{\text{GL}} % general linear group \newcommand{\SL}{\text{SL}} % special linear group \newcommand{\SO}{\text{SO}} % special orthogonal group \newcommand{\O}{\text{O}} % orthogonal group \newcommand{\SU}{\text{SU}} % special unitary group \newcommand{\Spin}{\text{Spin}} % Spin group \newcommand{\RP}{\Rr\mathrm P} % real projective space \newcommand{\CP}{\Cc\mathrm P} % complex projective space \newcommand{\HP}{\Hh\mathrm P} % quaternionic projective space \newcommand{\Top}{\mathrm{Top}} % topological category \newcommand{\PL}{\mathrm{PL}} % piecewise linear category \newcommand{\Cat}{\mathrm{Cat}} % any category \newcommand{\KS}{\text{KS}} % Kirby-Siebenmann class \newcommand{\Hud}{\text{Hud}} % Hudson torus \newcommand{\Ker}{\text{Ker}} % Kernel \newcommand{\underbar}{\underline} %Classifying Spaces for Families of Subgroups \newcommand{\textup}{\text} \newcommand{\sp}{^}r \neq 0$ then the complex is exact, hence acyclic. To compute the Reidemeister torsion we need to construct a chain homotopy 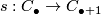$s: C_\bullet \to C_{\bullet+1}$$s: C_\bullet \to C_{\bullet+1}$ such that

$\displaystyle ds + sd = \id$ $$\displaystyle ds + sd = \id$$

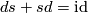
Here we can take 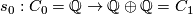$s_0 : C_0 = \Q \to \Q\oplus \Q = C_1$$s_0 : C_0 = \Q \to \Q\oplus \Q = C_1$ to be the map 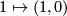$1 \mapsto (1,0)$$1 \mapsto (1,0)$ as then

$\displaystyle s_{-1}(d_0(x)) + d_1(s_0(x)) = d_1(x,0) = x$ $$\displaystyle s_{-1}(d_0(x)) + d_1(s_0(x)) = d_1(x,0) = x$$

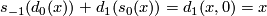
and then we need to choose 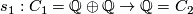$s_1: C_1 = \Q\oplus \Q \to \Q = C_2$$s_1: C_1 = \Q\oplus \Q \to \Q = C_2$ to be the map $(x,y) \mapsto \frac{y}{r}$$(x,y) \mapsto \frac{y}{r}$.

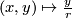To compute the torsion of this complex we have to consider the class

$\displaystyle \lbrack d+s : C_{\mathrm{ev}} \to C_{\mathrm{odd}} \rbrack \in K_1(\Q)$ $$\displaystyle \lbrack d+s : C_{\mathrm{ev}} \to C_{\mathrm{odd}} \rbrack \in K_1(\Q)$$

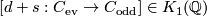
which is given by

$\displaystyle (d+s)(x,y) = d_2(x) + s_0(y) = (y,rx)$ $$\displaystyle (d+s)(x,y) = d_2(x) + s_0(y) = (y,rx)$$

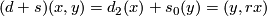
and hence the matrix of 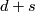$d+s$$d+s$ in the standard basis is given by

$\displaystyle A:=\begin{pmatrix} 0 & 1 \\ r & 0 \end{pmatrix},$ $$\displaystyle A:=\begin{pmatrix} 0 & 1 \\ r & 0 \end{pmatrix},$$

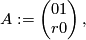
whose class in 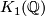$K_1(\Q)$$K_1(\Q)$ is the same as the class of 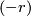$(-r)$$(-r)$ since

$\displaystyle A\simeq E_{12}^{-1}E_{21}^{1}AE_{21}^{-r}=\begin{pmatrix} -r & 0 \\ 0 & 1 \end{pmatrix} \simeq (-r)$ $$\displaystyle A\simeq E_{12}^{-1}E_{21}^{1}AE_{21}^{-r}=\begin{pmatrix} -r & 0 \\ 0 & 1 \end{pmatrix} \simeq (-r)$$

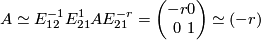
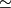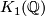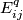where $\simeq$$\simeq$ stands for equality in $K_1(\Q)$$K_1(\Q)$ and $E_{ij}^q$$E_{ij}^q$ is the elementary matrix with 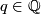$q\in\Q$$q\in\Q$ at the 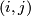$(i,j)$$(i,j)$ entry.