Reidemeister torsion (Ex)

Revision as of 10:49, 30 July 2013 (view source) Diarmuid Crowley (Talk | contribs) m ← Older edit		Latest revision as of 12:46, 31 August 2013 (view source) Markus Land (Talk | contribs)
Line 7:		Line 7:
	{{#RefList:}}		{{#RefList:}}
	[[Category:Exercises]]		[[Category:Exercises]]
−	[[Category:Exercises without solution]]	+	[[Category:Exercises with solution]]

---

Latest revision as of 12:46, 31 August 2013

Show that the following finite based free $<wikitex>; Show that the following finite based free $\Qq$-chain compex concentrated in dimensions $, \Qq$-chain compex concentrated in dimensions $2$, $1$ and $0$ is contractible and compute its Reidemeister torsion:

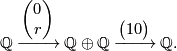
[edit] References

$ and $\Qq$-chain compex concentrated in dimensions $2$, $1$ and $0$ is contractible and compute its Reidemeister torsion:

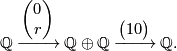
[edit] References

$ is contractible and compute its Reidemeister torsion: $$ \Qq \xrightarrow{\left( \begin{array}{c} 0 \ r \end{array} \right)} \Qq \oplus \Qq \xrightarrow{\left( \begin{array}{cc} 1 & 0 \end{array} \right)} \Qq. $$ == References == {{#RefList:}} [[Category:Exercises]] [[Category:Exercises with solution]]\Qq-chain compex concentrated in dimensions $2$, $1$ and $0$ is contractible and compute its Reidemeister torsion:

[edit] References