Quadratic forms I (Ex)
From Manifold Atlas
(Difference between revisions)
(Created page with "<wikitex>; We follow {{citeD|Lück2001|Definition 4.22}} Let $P$ be a finitely generated free $\Lambda$ module, $\Lambda$ a ring with involution. Let $$ T \colon \textup{Hom...") |
m |
||
| Line 9: | Line 9: | ||
{{endthm}} | {{endthm}} | ||
</wikitex> | </wikitex> | ||
| − | + | {{beginrem|Remark}} | |
| − | {{ | + | See also {{citeD|Ranicki1980|Section 2}}. |
| + | {{endrem}} | ||
[[Category:Exercises]] | [[Category:Exercises]] | ||
[[Category:Exercises without solution]] | [[Category:Exercises without solution]] | ||
Latest revision as of 18:22, 29 May 2012
We follow [Lück2001, Definition 4.22]
Let 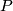 be a finitely generated free
be a finitely generated free 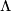 module,
module, 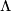 a ring with involution. Let
a ring with involution. Let
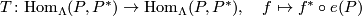
be the involution where 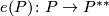 is the canonical isomorphism given by evaluation. Define
is the canonical isomorphism given by evaluation. Define

Exercise 0.1.
Show that 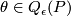 defines a unique
defines a unique  -quadratic form on
-quadratic form on 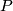 and that every such form arises in this way.
and that every such form arises in this way.
Remark 0.2. See also [Ranicki1980, Section 2].