Pseudoholomorphic curves
(Created page with "<!-- COMMENT: To achieve a unified layout, along with using the template below, please OBSERVE the following: besides, $...$ and $$...$$, you should use two environments: - Fo...") |
m |
||
| Line 18: | Line 18: | ||
Let $(\Sigma,j)$ be a Riemann surface with complex structure $j$. A '''$(j,J)$-holomorphic curve''' | Let $(\Sigma,j)$ be a Riemann surface with complex structure $j$. A '''$(j,J)$-holomorphic curve''' | ||
$$u\co\Sigma\rightarrow X$$ | $$u\co\Sigma\rightarrow X$$ | ||
| − | is a smooth map satisfying $du\circ j=J\circ du$ | + | is a smooth map satisfying |
| + | $$du\circ j=J\circ du$$ | ||
| + | or equivalently | ||
| + | $$\bar{\partial}_Ju\co =\frac{1}{2}(du+J\circ du\circ j)=0$$ | ||
| + | A $J$-holomorphic map is called '''simple''' if it cannot be factored as $u=v\circ\phi$ where $\phi$ is a $(j',j)$-holomorphic branched cover $\phi\co\Sigma'\rightarrow\Sigma$ of degree strictly greater than 1. We will usually omit $j$ from the notation and speak of $J$-holomorphic curves. The term '''pseudoholomorphic curve''' will be used to describe a $J$-holomorphic curve when we do not want to specify $J$. | ||
{{endthm}} | {{endthm}} | ||
Pseudoholomorphic curves provide a useful tool for studying [[symplectic manifolds]]. | Pseudoholomorphic curves provide a useful tool for studying [[symplectic manifolds]]. | ||
| + | == Taming $J$ == | ||
| + | Pseudoholomorphic curves in a general almost complex manifold can be quite wild (EXAMPLE?). Better behaviour can be ensured by the existence of a symplectic $\omega$ taming $J$, that is the quadratic form | ||
| + | $$g(v,w)=\omega(v,Jw)$$ | ||
| + | is positive-definite. This gives us topological control on the '''energy''' of a $J$-holomorphic curve | ||
| + | $$E(u)=\int_{\Sigma}|du|^2d\mathrm{vol}$$ | ||
| + | (here the norm and volume form are taken with respect to the metric $g$) thanks to the identity | ||
| + | $$E(u)=\int_{\Sigma}u^*\omega$$ | ||
| + | If moreover we require the metric $g$ to be $J$-invariant ($g(Jv,Jw)=g(v,w)$) then we say that $J$ is $\omega$-compatible and we have the identity | ||
| + | $$E(u)=\int_{\Sigma}|\partial_Ju|^2d\mathrm{vol}+\int_{\Sigma}u^*\omega$$ | ||
| + | so that the $J$-holomorphic curves are the absolute minima of the energy functional on the space of maps $\Sigma\rightarrow X$. | ||
| + | == Moduli spaces == | ||
| + | Simple $J$-holomorphic curves form nice moduli spaces | ||
| + | {{beginthm|Theorem|Transversality for simple curves}} | ||
| + | Fix a homology class $A\in H_2(X;\mathbb{Z})$ and a Riemann surface $(\Sigma,j)$. There is a subset $\mathcal{J}_{\mathrm{reg}}\subset\mathcal{J}$ of the second-category such that the space | ||
| + | $$\mathcal{M}^*(\Sigma,X;A,J)\co = \{u\co\Sigma\rightarrow X|du\circ j=J\circ du\}$$ | ||
| + | is a finite-dimensional manifold of dimension | ||
| + | $$n(2-2g)+2c_1(X,J)[A]$$ | ||
| + | {{endthm}} | ||
| + | These almost complex structures are the '''regular''' almost complex structures, for which the linearised problem has vanishing cokernel. Transversality is achieved by making small perturbations of the almost complex structure in regions through which the pseudoholomorphic curve has to pass. | ||
| + | == Compactness == | ||
| + | While the $L^2$-control on the derivatives of $u$ given by the energy identity is not enough to ensure a priori compactness of moduli spaces, there is a natural compactification by adding in strata of '''stable maps'''. | ||
| + | {{beginthm|Definition|(Stable map)}} | ||
| + | Let $(\Sigma,j)$ be a nodal Riemann surface (i.e. a connected, compact reduced complex curve with at worst ordinary double points) and $x_1,\ldots,x_k$ a collection of distinct non-nodal marked points on $\Sigma$. A stable map $u\co\Sigma\rightarrow X$ is a $J$-holomorphic map such that any irreducible component of $\Sigma$ which is mapped down to a point $x\in X$ has either | ||
| + | \begin{itemize} | ||
| + | \item arithmetic genus 0 and at least three points which are either marked or nodal, | ||
| + | \item arithmetic genus 1 and at least one point which is either marked or nodal, | ||
| + | \item arithmetic genus 2 or more. | ||
| + | |||
| + | \end{itemize} | ||
| + | This is equivalent to the requirement that the group of holomorphic automorphisms $\phi$ of $\Sigma$ fixing the marked points aznd satisfying $u\circ\phi=u$ is finite. | ||
| + | {{endthm}} | ||
| + | There is a notion of convergence for stable maps, called Gromov convergence, which allows us to define a topology of the space of stable maps. | ||
| + | {{beginthm|Theorem|(Gromov compactness)}} | ||
| + | The space of stable maps with the topology of Gromov convergence is both compact and Hausdorff. | ||
| + | {{endthm}} | ||
</wikitex> | </wikitex> | ||
Revision as of 13:04, 7 March 2011
|
This page has not been refereed. The information given here might be incomplete or provisional. |
1 Introduction
In this article, 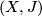 will denote an almost complex manifold of dimension
will denote an almost complex manifold of dimension  .
.
Definition 1.1 ( -holomorphic curve).
Let
-holomorphic curve).
Let 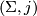 be a Riemann surface with complex structure
be a Riemann surface with complex structure  . A
. A 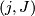 -holomorphic curve
-holomorphic curve
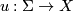
is a smooth map satisfying
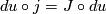
or equivalently
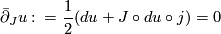
A  -holomorphic map is called simple if it cannot be factored as
-holomorphic map is called simple if it cannot be factored as 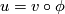 where
where  is a
is a 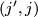 -holomorphic branched cover
-holomorphic branched cover 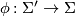 of degree strictly greater than 1. We will usually omit
of degree strictly greater than 1. We will usually omit  from the notation and speak of
from the notation and speak of  -holomorphic curves. The term pseudoholomorphic curve will be used to describe a
-holomorphic curves. The term pseudoholomorphic curve will be used to describe a  -holomorphic curve when we do not want to specify
-holomorphic curve when we do not want to specify  .
.
Pseudoholomorphic curves provide a useful tool for studying symplectic manifolds.
1 Taming 
Pseudoholomorphic curves in a general almost complex manifold can be quite wild (EXAMPLE?). Better behaviour can be ensured by the existence of a symplectic  taming
taming  , that is the quadratic form
, that is the quadratic form
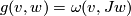
is positive-definite. This gives us topological control on the energy of a  -holomorphic curve
-holomorphic curve
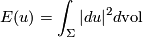
(here the norm and volume form are taken with respect to the metric  ) thanks to the identity
) thanks to the identity
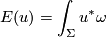
If moreover we require the metric  to be
to be  -invariant (
-invariant (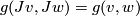 ) then we say that
) then we say that  is
is  -compatible and we have the identity
-compatible and we have the identity
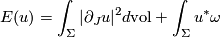
so that the  -holomorphic curves are the absolute minima of the energy functional on the space of maps
-holomorphic curves are the absolute minima of the energy functional on the space of maps  .
.
2 Moduli spaces
Simple  -holomorphic curves form nice moduli spaces
-holomorphic curves form nice moduli spaces
Theorem 5.1 Transversality for simple curves.
Fix a homology class 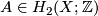 and a Riemann surface
and a Riemann surface 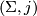 . There is a subset
. There is a subset 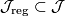 of the second-category such that the space
of the second-category such that the space
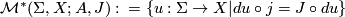
is a finite-dimensional manifold of dimension
![\displaystyle n(2-2g)+2c_1(X,J)[A]](/images/math/1/e/a/1eaaedc1211195624b75d18a0c41a504.png)
These almost complex structures are the regular almost complex structures, for which the linearised problem has vanishing cokernel. Transversality is achieved by making small perturbations of the almost complex structure in regions through which the pseudoholomorphic curve has to pass.
3 Compactness
While the  -control on the derivatives of
-control on the derivatives of  given by the energy identity is not enough to ensure a priori compactness of moduli spaces, there is a natural compactification by adding in strata of stable maps.
given by the energy identity is not enough to ensure a priori compactness of moduli spaces, there is a natural compactification by adding in strata of stable maps.
Definition 7.1 (Stable map).
Let 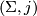 be a nodal Riemann surface (i.e. a connected, compact reduced complex curve with at worst ordinary double points) and
be a nodal Riemann surface (i.e. a connected, compact reduced complex curve with at worst ordinary double points) and 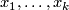 a collection of distinct non-nodal marked points on
a collection of distinct non-nodal marked points on  . A stable map
. A stable map 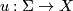 is a
is a  -holomorphic map such that any irreducible component of
-holomorphic map such that any irreducible component of  which is mapped down to a point
which is mapped down to a point 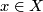 has either
\begin{itemize}
\item arithmetic genus 0 and at least three points which are either marked or nodal,
\item arithmetic genus 1 and at least one point which is either marked or nodal,
\item arithmetic genus 2 or more.
has either
\begin{itemize}
\item arithmetic genus 0 and at least three points which are either marked or nodal,
\item arithmetic genus 1 and at least one point which is either marked or nodal,
\item arithmetic genus 2 or more.
\end{itemize}
This is equivalent to the requirement that the group of holomorphic automorphisms  of
of  fixing the marked points aznd satisfying
fixing the marked points aznd satisfying 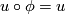 is finite.
is finite.
There is a notion of convergence for stable maps, called Gromov convergence, which allows us to define a topology of the space of stable maps.
Theorem 7.2 (Gromov compactness). The space of stable maps with the topology of Gromov convergence is both compact and Hausdorff.