Pseudoholomorphic curves
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
[edit] 1 Introduction
In this article, 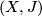 will denote an almost complex manifold of dimension
will denote an almost complex manifold of dimension  .
.
Definition 1.1 ( -holomorphic curve).
Let
-holomorphic curve).
Let 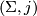 be a Riemann surface with complex structure
be a Riemann surface with complex structure  . A
. A  -holomorphic curve
-holomorphic curve
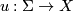
is a smooth map satisfying
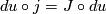
or equivalently
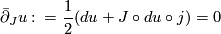
A  -holomorphic map is called simple if it cannot be factored as
-holomorphic map is called simple if it cannot be factored as 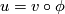 where
where  is a
is a  -holomorphic branched cover
-holomorphic branched cover 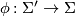 of degree strictly greater than 1. We will usually omit
of degree strictly greater than 1. We will usually omit  from the notation and speak of
from the notation and speak of  -holomorphic curves. The term pseudoholomorphic curve will be used to describe a
-holomorphic curves. The term pseudoholomorphic curve will be used to describe a  -holomorphic curve when we do not want to specify
-holomorphic curve when we do not want to specify  .
.
Pseudoholomorphic curves provide a useful tool for studying symplectic manifolds.
[edit] 2 Taming J
Pseudoholomorphic curves in a general almost complex manifold can be quite wild (EXAMPLE?). Better behaviour can be ensured by the existence of a symplectic  taming
taming  , that is the quadratic form
, that is the quadratic form
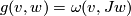
is positive-definite. This gives us topological control on the energy of a  -holomorphic curve
-holomorphic curve
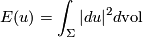
(here the norm and volume form are taken with respect to the metric  ) thanks to the identity
) thanks to the identity
Lemma 2.1 (Energy identity).
If  is a
is a  -holomorphic curve and
-holomorphic curve and  is tamed by
is tamed by  then
then
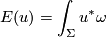
If moreover we require the metric  to be
to be  -invariant (
-invariant (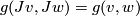 ) then we say that
) then we say that  is
is  -compatible and we have the identity
-compatible and we have the identity
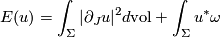
so that the  -holomorphic curves are the absolute minima of the energy functional on the space of maps
-holomorphic curves are the absolute minima of the energy functional on the space of maps 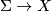 .
.
[edit] 3 Linearisation
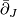 as a section of a Banach bundle. Explicitly, let
as a section of a Banach bundle. Explicitly, let 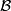 denote the
denote the 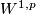 -completion of the space of maps
-completion of the space of maps 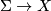 and let
and let 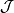 denote the space of
denote the space of  -compatible almost complex structures. Define the Banach bundle
-compatible almost complex structures. Define the Banach bundle 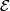 over
over 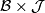 whose fibre over
whose fibre over 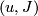 is the
is the 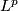 -completion of the space
-completion of the space 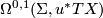
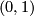 -forms on
-forms on  with values in
with values in 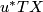 . Here
. Here 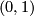 refers to the complex structures
refers to the complex structures  on
on 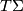 and
and  on
on 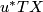 . By definition,
. By definition, 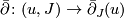 is a section of this bundle over the smooth locus and it extends naturally to the Sobolev completions.
is a section of this bundle over the smooth locus and it extends naturally to the Sobolev completions. 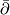 at a
at a  -holomorphic curve
-holomorphic curve  is the operator
is the operator 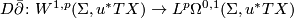
 on
on  ) by
) by 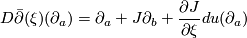
Here we think of  as a section of
as a section of  and
and 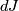 as a map
as a map 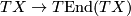 so
so 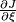 means the pushforward of
means the pushforward of  along
along 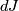 . The linearisation measures to first order the change in
. The linearisation measures to first order the change in 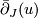 when
when  is deformed along a vector field
is deformed along a vector field  . One can also allow
. One can also allow  to vary in the space of complex structures on
to vary in the space of complex structures on  or
or  to vary in a family of almost complex structures by adding corresponding terms to the linearisation.
to vary in a family of almost complex structures by adding corresponding terms to the linearisation.
Theorem 3.2 Ellipticity. The linearised Cauchy-Riemann operator of a holomorphic curve is a Fredholm operator.
In the case when  is an integrable complex structure the kernel and cokernel of the linearised Cauchy-Riemann operator agree with the usual Dolbeault cohomology groups.
is an integrable complex structure the kernel and cokernel of the linearised Cauchy-Riemann operator agree with the usual Dolbeault cohomology groups.
[edit] 4 Moduli spaces
Simple  -holomorphic curves form nice moduli spaces
-holomorphic curves form nice moduli spaces
Theorem 4.1 Transversality for simple curves.
Fix a homology class 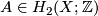 and a Riemann surface
and a Riemann surface 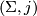 . There is a subset
. There is a subset 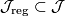 of the second-category such that the space
of the second-category such that the space
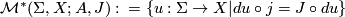
is a finite-dimensional manifold of dimension
![\displaystyle n(2-2g)+2c_1(X,J)[A]](/images/math/1/e/a/1eaaedc1211195624b75d18a0c41a504.png)
If one allows  to vary then this dimension formula gains an extra
to vary then this dimension formula gains an extra 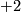 if
if 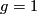 or
or 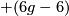 if
if 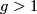 .
.
These almost complex structures are the regular almost complex structures, for which the linearised problem has vanishing cokernel. Transversality is achieved by making small perturbations of the almost complex structure in regions through which the pseudoholomorphic curve has to pass.
Usually one defines a moduli space by dividing out the space of parametrised maps by the group of holomorphic reparametrisations. This group is:
-
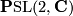 , the 6-dimensional group of M\"{o}bius transformations when
, the 6-dimensional group of M\"{o}bius transformations when 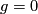 ,
,
-
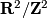 , acting by translations when
, acting by translations when 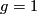 ,
,
- finite when
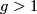
Definition 4.2 Expected dimension. The expected dimension of the moduli space is the number
![\displaystyle n(2-2g)+2c_1(X,J)[A]+6g-6](/images/math/6/3/d/63d76165355535a5651d2ed3570fc8c8.png)
and this coincides with the actual dimension of a regular moduli space of curves after dividing out by reparametrisation.
It is harder to achieve transversality for curves which are multiple covers. This is best seen in a simple example.
Example 4.3 Isolated spheres in Calabi-Yau 3-folds.
Consider  , the total space of the bundle
, the total space of the bundle 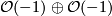 over
over 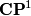 . The inclusion of the zero-section
. The inclusion of the zero-section 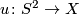 is the only closed holomorphic curve in its homology class (up to reparametrisation). This sphere is regular; the expected dimension is zero since
is the only closed holomorphic curve in its homology class (up to reparametrisation). This sphere is regular; the expected dimension is zero since 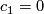 . If
. If 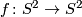 is a generic holomorphic branched cover of degree
is a generic holomorphic branched cover of degree  then
then  lives in a moduli space of dimension
lives in a moduli space of dimension 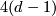 (corresponding to the configuration space of the
(corresponding to the configuration space of the 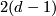 branch points). The expected dimension is still zero, so the linearised operator must have a nontrivial cokernel.
branch points). The expected dimension is still zero, so the linearised operator must have a nontrivial cokernel.
In this case one needs to introduce more general perturbations to achieve transversality.
Theorem 4.4 Transversality in the semipositive case.
When 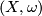 is semipositive one can achieve transversality even for multiply-covered curves by using a domain-dependent
is semipositive one can achieve transversality even for multiply-covered curves by using a domain-dependent  .
.
[edit] 5 Compactness
While the  -control on the derivatives of
-control on the derivatives of  given by the energy identity 2.1 is not enough to ensure a priori compactness of moduli spaces, there is a natural compactification by adding in strata of stable maps.
given by the energy identity 2.1 is not enough to ensure a priori compactness of moduli spaces, there is a natural compactification by adding in strata of stable maps.
Definition 5.1 (Stable map).
Let 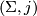 be a nodal Riemann surface (i.e. a connected, compact reduced complex curve with at worst ordinary double points) and
be a nodal Riemann surface (i.e. a connected, compact reduced complex curve with at worst ordinary double points) and 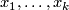 a collection of distinct non-nodal marked points on
a collection of distinct non-nodal marked points on  . A stable map
. A stable map 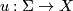 is a
is a  -holomorphic map such that any irreducible component of
-holomorphic map such that any irreducible component of  which is mapped down to a point
which is mapped down to a point 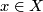 has either
has either
- arithmetic genus 0 and at least three points which are either marked or nodal,
- arithmetic genus 1 and at least one point which is either marked or nodal,
- arithmetic genus 2 or more.
This is equivalent to the requirement that the group of holomorphic automorphisms  of
of  fixing the marked points and satisfying
fixing the marked points and satisfying 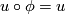 is finite. A reparametrisation of a stable map is a holomorphic automorphism of the domain which does not necessarily leave
is finite. A reparametrisation of a stable map is a holomorphic automorphism of the domain which does not necessarily leave  invariant and we usually only consider stable maps up to reparametrisation.
invariant and we usually only consider stable maps up to reparametrisation.
There is a notion of convergence for stable maps up to reparametrisation, called Gromov convergence, which allows us to define a topology of the moduli space of stable maps.
Theorem 5.2 (Gromov compactness). The moduli space of stable maps (modulo reparametrisations) with the topology of Gromov convergence is both compact and Hausdorff.