Poincaré duality IV (Ex)
From Manifold Atlas
Revision as of 22:37, 22 March 2012 by Diarmuid Crowley (Talk | contribs)
Exercise 0.1.
Let 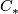 and
and 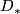 be
be 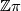 -chain complexes and
-chain complexes and
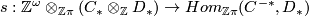
be defined by sending 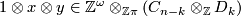 to the map
to the map
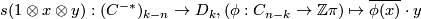
Show that  is a
is a  -chain map.
-chain map.
Hint: Note that 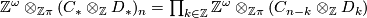 with boundary map
with boundary map 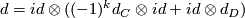 and
and 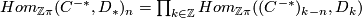 with boundary map
with boundary map 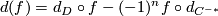 .
.
The exercises and hints on this page were sent by Alex Koenen and Arkadi Schelling.