Poincaré duality IV (Ex)
Exercise 0.1.
Let 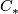 and
and 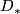 be
be 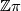 -chain complexes and
-chain complexes and
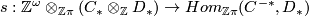
be defined by sending 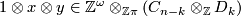 to the map
to the map
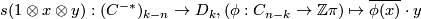
Show that  is a
is a  -chain map.
-chain map.
Hint: Note that 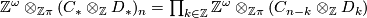 with boundary map
with boundary map 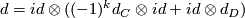 and that
and that 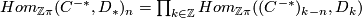 with boundary map
with boundary map 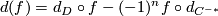 .
.
Exercise 0.2.
Let 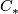 and
and 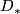 be
be 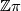 -chain complexes. Show that for the
-chain complexes. Show that for the  -th homology of the complex
-th homology of the complex 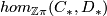 we have
we have
![\displaystyle H_n(hom_{\Zz\pi}(C_*,D_*))= [ \Sigma^n C_*,D_*]_{\Zz\pi}](/images/math/3/2/c/32c77545e74e241c649298b28c812e41.png)
where 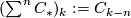 denotes the shifted complex with boundary map
denotes the shifted complex with boundary map 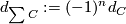 .
.
Hint: use the boundary map of Exercise 0.1.
Exercise 0.3.
Deduce from the Poincare homotopy equivalence ![? \cap [X]:C^{n-*}(\widetilde X) \rightarrow C_*(\widetilde X)](/images/math/8/8/f/88f3dd23bde01158059731d4e5a1ff41.png) that
that
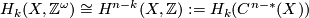
as  -Modules.
-Modules.
Exercise 0.4.
Let 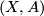 be a Poincare pair with
be a Poincare pair with  an
an  -dimensional, connected, finite CW-complex and
-dimensional, connected, finite CW-complex and 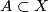 an
an  -dimensional subcomplex, an orientation homomorphism
-dimensional subcomplex, an orientation homomorphism 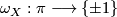 and a fundamental class
and a fundamental class ![[X,A]\in H_n(X,A;\Zz^{\omega_X}):=H_n(\Zz^{\omega_X}\otimes_{\Zz\pi}C_*(\tilde{X},\tilde{A}))](/images/math/9/d/6/9d61f4d9a9a95854e4942391d61dbf71.png) . That means, for a universal covering
. That means, for a universal covering 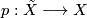 and
and 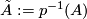 the
the 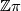 -chain maps
-chain maps ![?\cap [X,A]:C^{n-*}(\tilde{X},\tilde{A})\longrightarrow C_*(\tilde{X})](/images/math/2/4/2/24291e86ad4c8d791398702c1a993b88.png) and
and ![?\cap [X,A]:C^{n-*}(\tilde{X})\longrightarrow C_*(\tilde{X},\tilde{A})](/images/math/7/2/4/724d59eacb8ebe40d4bd3fc4be37e27f.png) are
are 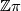 -chain homotopy equivalences.
-chain homotopy equivalences.
Show that the components 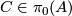 of
of  inherit the structure of a finite
inherit the structure of a finite  -dimensional Poincare complex, i.e. that there is an induced orientation homomorphism
-dimensional Poincare complex, i.e. that there is an induced orientation homomorphism 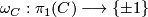 and an induced fundamental class
and an induced fundamental class ![[C]\in H_{n-1}(C;\Zz^{\omega_C})](/images/math/e/7/8/e7858d2c27fad4c2cac03b4444e737fa.png) , such that
, such that
![\displaystyle ?\cap [C]:C^{n-1-*}(\tilde{C})\longrightarrow C_*(\tilde{C})](/images/math/2/3/2/232581f0c3bb2b6b4be216d2dbd47adc.png)
is a 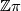 -chain homotopy equivalence.
-chain homotopy equivalence.
Hint: Tensorize both sides with 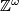 and consider the induced map.
and consider the induced map.
The exercises and hints on this page were sent by Alex Koenen and Arkadi Schelling.