Poincaré duality IV (Ex)
m |
m |
||
| (4 intermediate revisions by 2 users not shown) | |||
| Line 9: | Line 9: | ||
'''Hint''': Note that $ \Zz^{\omega} \otimes_{\Zz \pi}(C_* \otimes_{\Zz} D_*)_n=\prod_{k \in \Zz} \Zz^{\omega} \otimes_{\Zz\pi}(C_{n-k} \otimes_{\Zz} D_k) $ with boundary map $ d=id \otimes ((-1)^kd_C \otimes id + id \otimes d_D) $ and that $Hom_{\Zz\pi}(C^{-*},D_*)_n=\prod_{k \in \Zz}Hom_{\Zz\pi}((C^{-*})_{k-n},D_k)$ with boundary map $d(f)=d_D \circ f-(-1)^nf \circ d_{C^{-*}}$. | '''Hint''': Note that $ \Zz^{\omega} \otimes_{\Zz \pi}(C_* \otimes_{\Zz} D_*)_n=\prod_{k \in \Zz} \Zz^{\omega} \otimes_{\Zz\pi}(C_{n-k} \otimes_{\Zz} D_k) $ with boundary map $ d=id \otimes ((-1)^kd_C \otimes id + id \otimes d_D) $ and that $Hom_{\Zz\pi}(C^{-*},D_*)_n=\prod_{k \in \Zz}Hom_{\Zz\pi}((C^{-*})_{k-n},D_k)$ with boundary map $d(f)=d_D \circ f-(-1)^nf \circ d_{C^{-*}}$. | ||
| − | + | ||
| + | |||
| + | {{beginthm|Exercise}} \label{homol_hom} | ||
| + | Let $ C_* $ and $ D_* $ be $ \Zz\pi $-chain complexes. Show that for the $ n $-th homology of the complex $ hom_{\Zz\pi}(C_*,D_*) $ we have | ||
| + | $$ H_n(hom_{\Zz\pi}(C_*,D_*))= [ \Sigma^n C_*,D_*]_{\Zz\pi} $$ | ||
| + | where $ (\sum^nC_*)_k:=C_{k-n} $ denotes the shifted complex with boundary map $ d_{\sum C}:=(-1)^nd_C $. | ||
| + | {{endthm}} | ||
| + | |||
| + | '''Hint''': use the boundary map of Exercise \ref{chain_map}. | ||
| + | |||
| + | {{beginthm|Exercise}} | ||
| + | Deduce from the Poincare homotopy equivalence $ ? \cap [X]:C^{n-*}(\widetilde X) \rightarrow C_*(\widetilde X) $ that | ||
| + | $$ H_k(X,\Zz^{\omega}) \cong H^{n-k}(X,\Zz):=H_k(C^{n-*}(X)) $$ | ||
| + | as $ \Zz $-Modules. | ||
| + | {{endthm}} | ||
| + | |||
| + | {{beginthm|Exercise}} | ||
| + | Let $(X,A)$ be a Poincare pair with $X$ an $n$-dimensional, connected, finite CW-complex and $A\subset X$ an $(n-1)$-dimensional subcomplex, an orientation homomorphism $\omega_X : \pi \longrightarrow \{\pm 1\}$ and a fundamental class $[X,A]\in H_n(X,A;\Zz^{\omega_X}):=H_n(\Zz^{\omega_X}\otimes_{\Zz\pi}C_*(\tilde{X},\tilde{A}))$. That means, for a universal covering $p:\tilde{X}\longrightarrow X$ and $\tilde{A}:=p^{-1}(A)$ the $\Zz\pi$-chain maps $?\cap [X,A]:C^{n-*}(\tilde{X},\tilde{A})\longrightarrow C_*(\tilde{X})$ and $?\cap [X,A]:C^{n-*}(\tilde{X})\longrightarrow C_*(\tilde{X},\tilde{A})$ are $\Zz\pi$-chain homotopy equivalences. | ||
| + | |||
| + | Show that the components $C\in\pi_0(A)$ of $A$ inherit the structure of a finite $(n-1)$-dimensional Poincare complex, i.e. that there is an induced orientation homomorphism $\omega_C : \pi_1(C) \longrightarrow \{\pm 1\}$ and an induced fundamental class $[C]\in H_{n-1}(C;\Zz^{\omega_C})$, such that | ||
| + | $$ ?\cap [C]:C^{n-1-*}(\tilde{C})\longrightarrow C_*(\tilde{C})$$ | ||
| + | is a $\Zz\pi$-chain homotopy equivalence. | ||
| + | {{endthm}} | ||
| + | |||
| + | '''Hint''': Tensorize both sides with $ \Zz^{\omega} $ and consider the induced map. | ||
The exercises and hints on this page were sent by Alex Koenen and Arkadi Schelling. | The exercises and hints on this page were sent by Alex Koenen and Arkadi Schelling. | ||
| − | == References == | + | </wikitex> |
| − | {{#RefList:}} | + | <!-- == References == |
| + | {{#RefList:}} --> | ||
[[Category:Exercises]] | [[Category:Exercises]] | ||
| + | [[Category:Exercises without solution]] | ||
Latest revision as of 14:57, 1 April 2012
Exercise 0.1.
Let 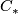 and
and 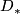 be
be 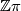 -chain complexes and
-chain complexes and
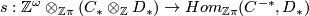
be defined by sending 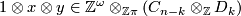 to the map
to the map
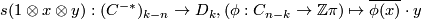
Show that  is a
is a 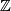 -chain map.
-chain map.
Hint: Note that 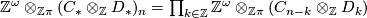 with boundary map
with boundary map 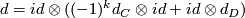 and that
and that 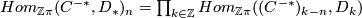 with boundary map
with boundary map 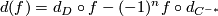 .
.
Exercise 0.2.
Let 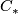 and
and 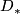 be
be 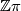 -chain complexes. Show that for the
-chain complexes. Show that for the 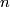 -th homology of the complex
-th homology of the complex 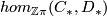 we have
we have
![\displaystyle H_n(hom_{\Zz\pi}(C_*,D_*))= [ \Sigma^n C_*,D_*]_{\Zz\pi}](/images/math/3/2/c/32c77545e74e241c649298b28c812e41.png)
where 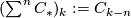 denotes the shifted complex with boundary map
denotes the shifted complex with boundary map 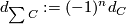 .
.
Hint: use the boundary map of Exercise 0.1.
Exercise 0.3.
Deduce from the Poincare homotopy equivalence ![? \cap [X]:C^{n-*}(\widetilde X) \rightarrow C_*(\widetilde X)](/images/math/8/8/f/88f3dd23bde01158059731d4e5a1ff41.png) that
that
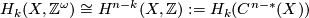
as 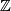 -Modules.
-Modules.
Exercise 0.4.
Let 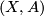 be a Poincare pair with
be a Poincare pair with 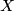 an
an 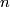 -dimensional, connected, finite CW-complex and
-dimensional, connected, finite CW-complex and 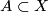 an
an 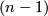 -dimensional subcomplex, an orientation homomorphism
-dimensional subcomplex, an orientation homomorphism 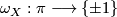 and a fundamental class
and a fundamental class ![[X,A]\in H_n(X,A;\Zz^{\omega_X}):=H_n(\Zz^{\omega_X}\otimes_{\Zz\pi}C_*(\tilde{X},\tilde{A}))](/images/math/9/d/6/9d61f4d9a9a95854e4942391d61dbf71.png) . That means, for a universal covering
. That means, for a universal covering 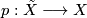 and
and 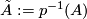 the
the 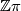 -chain maps
-chain maps ![?\cap [X,A]:C^{n-*}(\tilde{X},\tilde{A})\longrightarrow C_*(\tilde{X})](/images/math/2/4/2/24291e86ad4c8d791398702c1a993b88.png) and
and ![?\cap [X,A]:C^{n-*}(\tilde{X})\longrightarrow C_*(\tilde{X},\tilde{A})](/images/math/7/2/4/724d59eacb8ebe40d4bd3fc4be37e27f.png) are
are 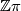 -chain homotopy equivalences.
-chain homotopy equivalences.
Show that the components 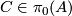 of
of 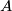 inherit the structure of a finite
inherit the structure of a finite 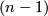 -dimensional Poincare complex, i.e. that there is an induced orientation homomorphism
-dimensional Poincare complex, i.e. that there is an induced orientation homomorphism 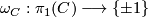 and an induced fundamental class
and an induced fundamental class ![[C]\in H_{n-1}(C;\Zz^{\omega_C})](/images/math/e/7/8/e7858d2c27fad4c2cac03b4444e737fa.png) , such that
, such that
![\displaystyle ?\cap [C]:C^{n-1-*}(\tilde{C})\longrightarrow C_*(\tilde{C})](/images/math/2/3/2/232581f0c3bb2b6b4be216d2dbd47adc.png)
is a 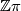 -chain homotopy equivalence.
-chain homotopy equivalence.
Hint: Tensorize both sides with 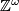 and consider the induced map.
and consider the induced map.
The exercises and hints on this page were sent by Alex Koenen and Arkadi Schelling.